Back to Home Page

1. Group Assingment

The full group assignment can be found here

I started the week working on installation of the firmware in the controller thereafter, I though I could use more practice in CAD design and switch to the design of the Gondola.

Ender II Firmware installation

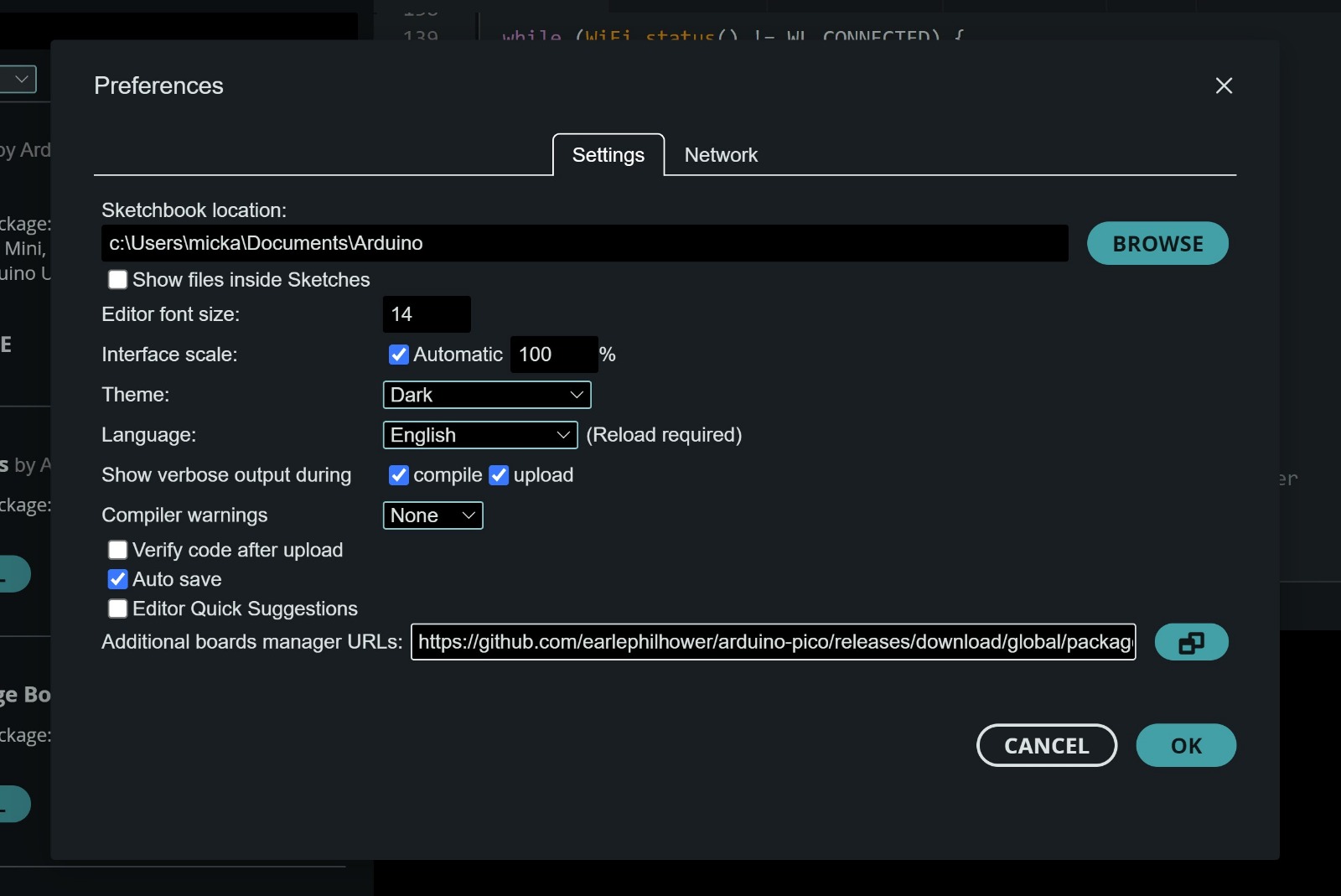
Initially, we attempted to re purpose the controller from an old Ender 2 for our project. I removed the controller board along with some of the motors. Our first task was to install new firmware onto the controller board.

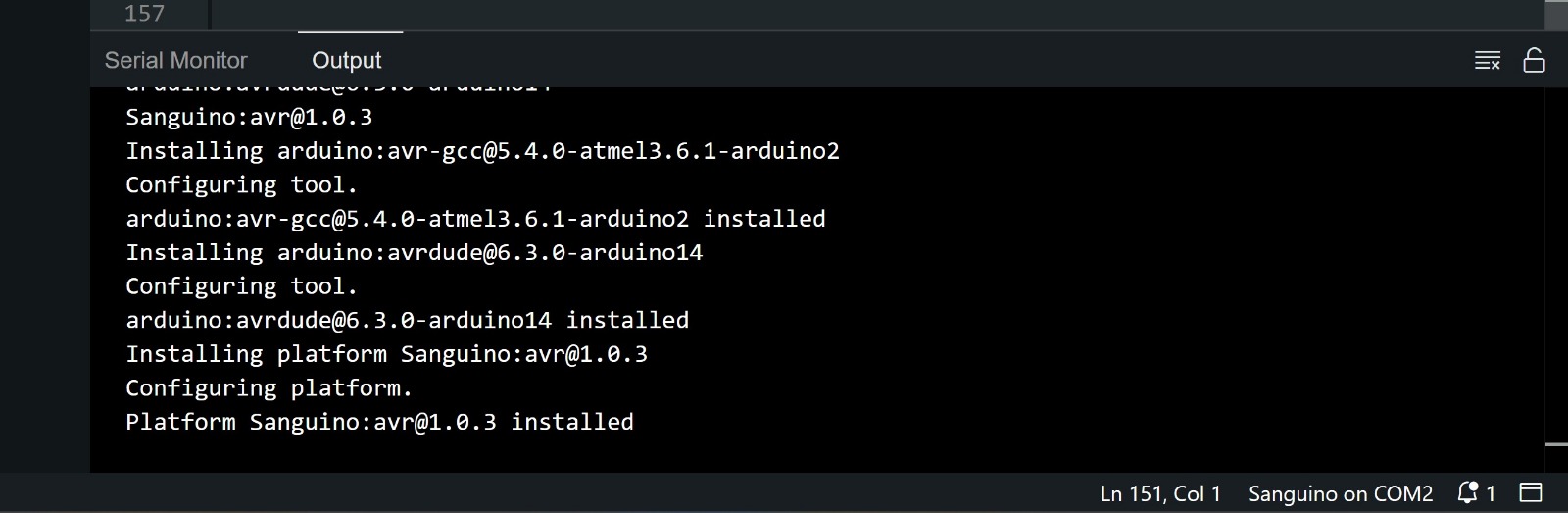
There were several possible versions of the controller board, but we identified ours as the one based on the ATmega1284P. After that, we asked ChatGPT how to install the firmware, and it directed us to this site:

First, we attempted to install the firmware using the Arduino IDE. Unfortunately, the controller was not recognized by the IDE.

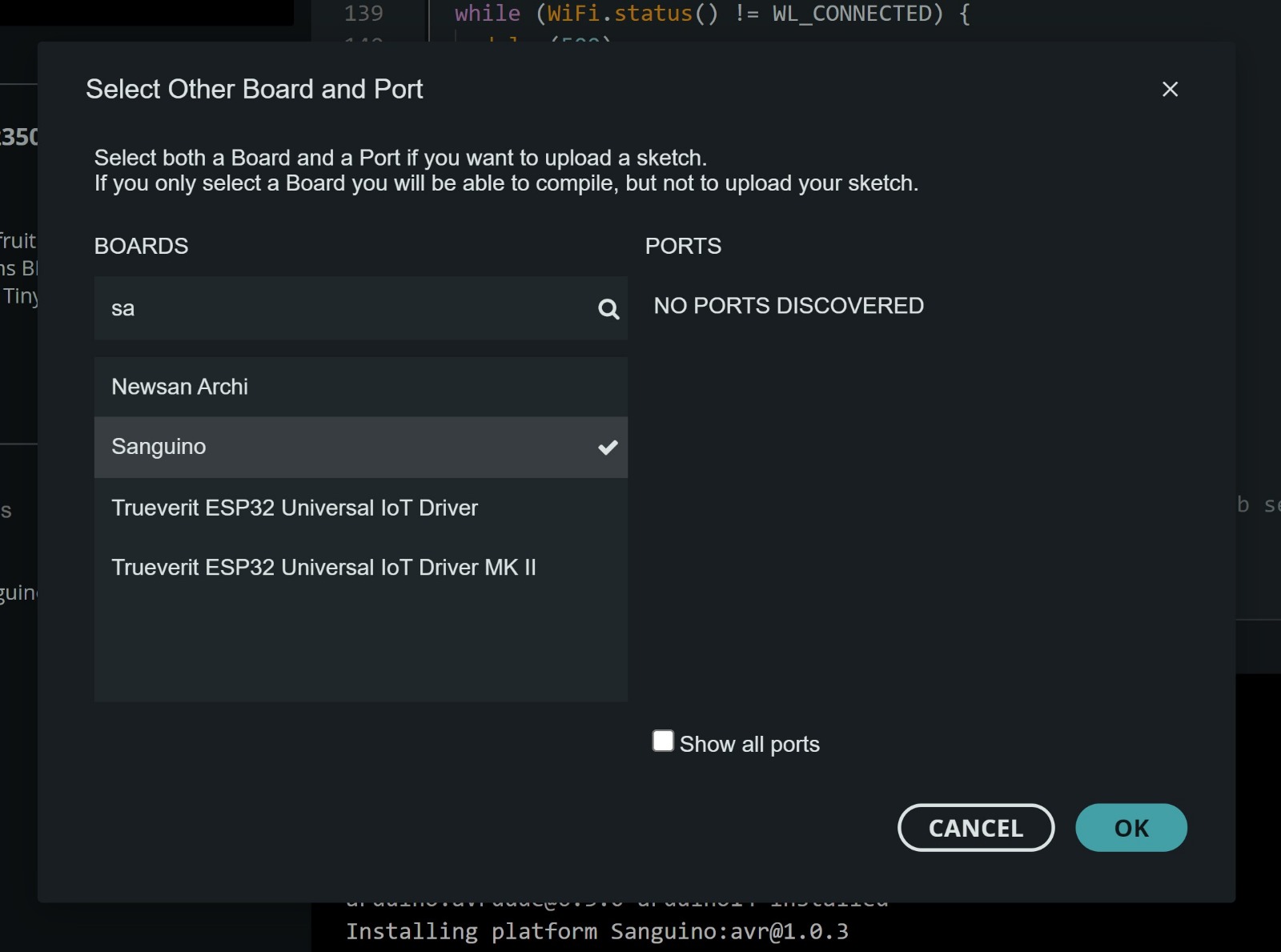
Next, we attempted to use an Arduino Uno as a bootloader by connecting its ICSP port to the ISP header on the Ender’s controller board. Unfortunately, this method was also unsuccessful, and we were still unable to install the firmware.

Finally, we decided to use specific pins on the Arduino Uno to connect directly to the ISP header on the Ender’s controller board, as shown in the picture below.

Luckily, this method worked. The issue earlier was likely due to a mismatch between the ISP pins on the Arduino and those on the Ender’s controller board.

The steps from the IDE side to install the software were:

Here the board firmawer was dowloaded from:

Sanguino firmware

Thereafter, we tried to install a software to see if we could blink a led.

This took a while as the information in regards to which pin was connected to the pin was not available. We had to install the program through arduino using Arduino as a programmer.

Gondola

The gondola is a base that is attached to the servo motors using belts or threads. It holds both a pen for drawing and a motor for lifting the pen.

For the pen-lifting mechanism, I explored various designs and found this one particularly interesting (link).

I designed the gondola in Fusion 360, focusing on three key elements:

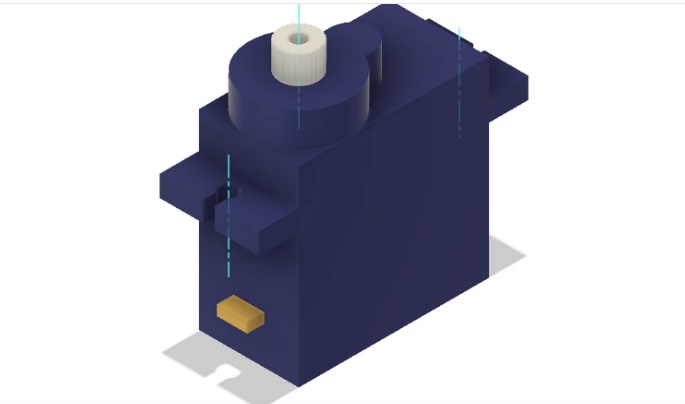
The motor used for lifting the pen is micro servo SG90 from an Arduino kit:

To accurately position the motor within the gondola, I used a Fusion 360 model I found online as a reference (link)

Penholder

In Fusion 360, I built the components using parametric design, allowing me to easily modify the bodies as needed. Below, you can see the sketch of the pen holder along with its sleeve.

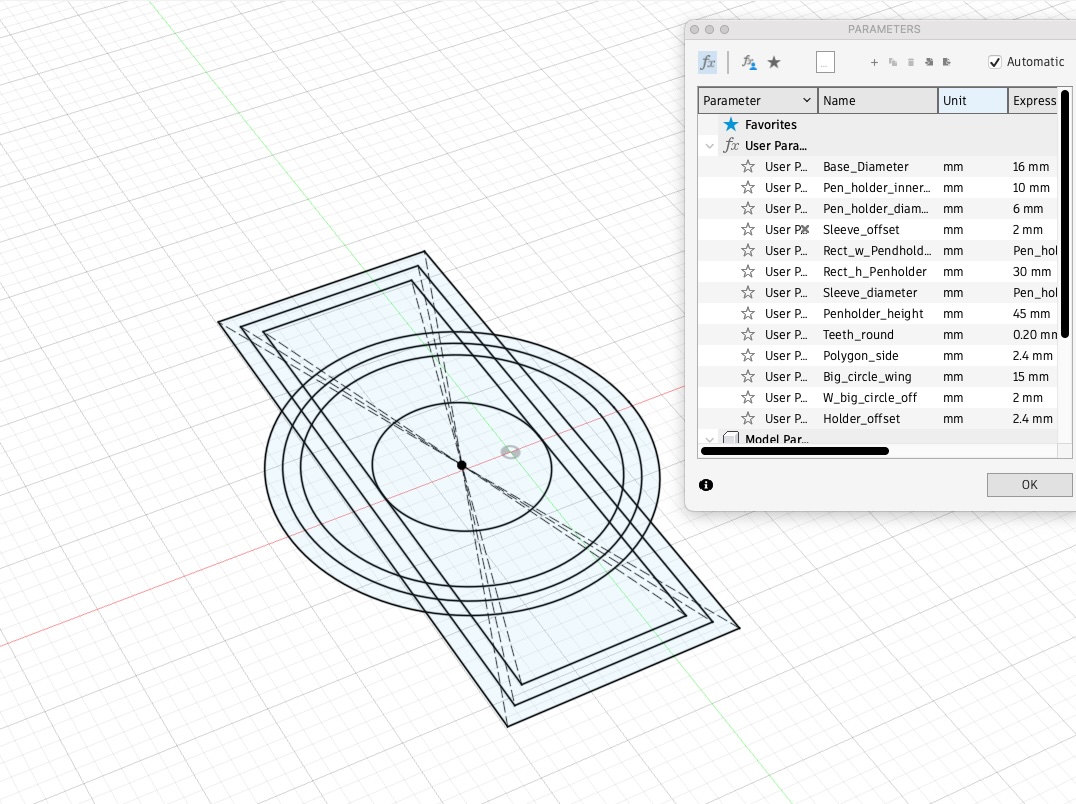
Afterward, I designed and built the pen lifter piece. To do this, I created a gear-shaped outline to cut into the pen lifter piece, allowing it to securely fit onto the motor shaft.

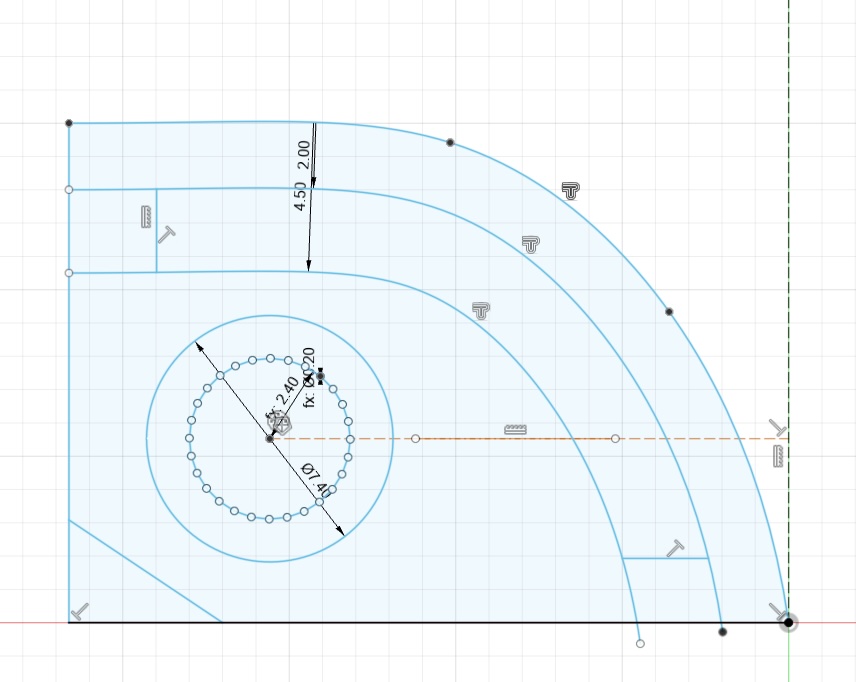
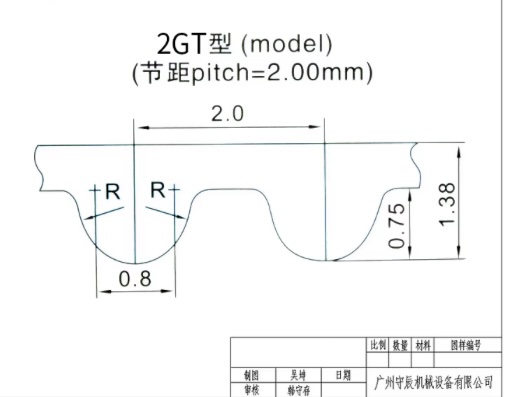
Next, I designed two round belt holders. The groove that holds the belt features a dented pattern, created by drawing a series of triangles to match the tooth profile of a 6 mm wide GT2 timing belt.

Here, you can find a belt fit test.

Finally, here is the finished model. I added fillets to the pen holder to make its insertion into the sleeve smoother and easier.

Then I proceeded to print the gondola in a bambulab 3d printer.


For the pen holder, I added a metal insert, allowing a bolt to securely hold the pen in place.

To determine the correct angle for the servo motor, I used the following Python script and followed its accompanying instructions (link).

# More details can be found in TechToTinker.blogspot.com 
# George Bantique | tech.to.tinker@gmail.com

from machine import Pin
from machine import PWM
from time import sleep_ms

def map(x, in_min, in_max, out_min, out_max):
    return int((x - in_min) * (out_max - out_min) / (in_max - in_min) + out_min)
    
class GORILLACELL_SERVO:
    def __init__(self, signal_pin):
        self.pwm = PWM(Pin(signal_pin), freq=50, duty=0)

    def rotate(self, angle):
        self.pwm.duty(map(angle, 0, 180, 23, 124))
        

servo = GORILLACELL_SERVO(signal_pin=25)

# The following lines of codes can be tested using the REPL:
# # To rotate the servo motor to 0 degrees
# servo.rotate(0)
# 
# # To rotate the servo motor to 90 degrees
# servo.rotate(90)
# 
# # To rotate the servo motor to 180 degrees
# servo.rotate(180)
# 
# # To rotate the servo from 0 to 180 degrees
# # by 10 degrees increment
# for angle in range(0, 181, 10):
#     servo.rotate(angle)
#     print(angle)
#     sleep_ms(500)
# # To rotate the servo from 180 to 0 degrees
# # by 10 degrees decrement
# for angle in range(180, -1, -10):
#     servo.rotate(angle)
#     print(angle)
#     sleep_ms(500)


Below you can find a test of the pen lifting mechanism

Then we went on installign the last printed version of the Gondola on to the structure that was built. For this a couple of 6mm belts were attached connecting it to the 2 stepper motors.

We used some nuts and bolts to find the right balance of the gondola on the structure system previously built.

Finally, after full implementation we could see that the pen would touch the paper.

Testing

We tested drawing a circle and a square with diameter and sides of 30 mm and 15 mm in Inskape. However, the resulting shapes measured 7.5 mm in diameter for the circle and 5 mm for the square. Increasing the step size by two, we obtained a circle with a 15 mm diameter and a square with a 10 mm side. When we doubled the step size, the dimensions of both objects remained unchanged.”

Micropython Polargraph

prompt give me the math for polargraph

A polargraph (or polar plotter) is a type of drawing machine that works using two stepper motors, typically mounted at the top corners of a board. A pen is suspended by strings (or belts) attached to the motors, and the pen’s position is determined by the lengths of these strings.

To control a polargraph, you need math to convert between Cartesian coordinates (x,y) and the string lengths L1 and L2 going to the motors.

Lets define

Motor 1 at (0,0) Motor 2 at (w,0) where w is the distance between the motors Pen at (x,y) measured from Motor 1.

\[L_1=x^2+y^2\]

\[L_2=\sqrt{(w-x)^2+y^2}\]

Where L1 amd L2 are the lengths we want to sove for (x,y)

This is a circle intersection problem:

circle 1: center at (0,0) radius L1 circle 2: center at (0,0) radius L2

find the distance between the motor centers

d=w

\[ a = \frac{L^2_{1}-L_{2}^2+d^2}{2d} \] \[ h = \sqrt{L_{1}^2-a^2} \]

Here is an example

for pen coordinates:

x=a

y=h

motors w=300 apart pen is at (150,100)

L1 = sqrt(1502+1002) = 180.28 L2 = sqrt(3000-150) = 180.28

Then I went onto translating GCODE into coordinates for this I wrote a short program in python. GCODE specifies the cutting or printing instructions with the prefix G01 or G1 and the movement i.e. no cutting with a G0.

Here is the code:

import re
import os
import matplotlib.pyplot as plt
def parse_gcode_line(line):
    gcodes = []
    x_vals = []
    y_vals = []
    for line in lines:
        if (line.startswith("G0") or line.startswith("G1")):    
            match = re.search(r'(G\d+)\s*X([-\d.]+)\s*Y([-\d.]+)', line)
            if match:
                gcodes.append(match.group(1))
                x_vals.append(float(match.group(2)))
                y_vals.append(float(match.group(3)))
    return gcodes, x_vals, y_vals
os.chdir("/Users/alfredorios/Documents/Fab_Academy/Gcode")
f = open("raven-outline_scaled.gcode", "r")
lines = f.readlines()
gcode,xcoord,ycoord=parse_gcode_line(lines)

here we plot the gcode

plt.plot(xcoord, ycoord)
plt.title("Gcode path")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.grid(True)
plt.show()

and here we save it to be used in the xiao S3

rows = zip(gcode,xcoord,ycoord)
print(rows)
import csv
with open('gcode_data.csv', 'w', newline='') as csvfile:
   writer = csv.writer(csvfile)
   writer.writerow(['G', 'X', 'Y'])  # optional header
   writer.writerows(rows)

Here is the code for a stepper motor library.

import time
from machine import Pin

class StepMotor:
    def __init__(self, pins):
        self.IN1 = Pin(pins[0], Pin.OUT)
        self.IN2 = Pin(pins[1], Pin.OUT)
        self.IN3 = Pin(pins[2], Pin.OUT)
        self.IN4 = Pin(pins[3], Pin.OUT)

        self.coilPins = [self.IN1, self.IN2, self.IN3, self.IN4]
        self.steps_per_rev = 4096/8
        self.angle = 0

        self.seq = [
            [1, 0, 0, 1],
            [1, 0, 0, 0],
            [1, 1, 0, 0],
            [0, 1, 0, 0],
            [0, 1, 1, 0],
            [0, 0, 1, 0],
            [0, 0, 1, 1],
            [0, 0, 0, 1]
        ]

    def step(self, angle, direction):
        steps = int((angle / 360.0) * self.steps_per_rev)
        if direction == 0:
            for _ in range(steps):
                for j in reversed(range(8)):
                    for pin in range(4):
                        self.coilPins[pin].value(self.seq[j][pin])
                    time.sleep_ms(2)
        else:
            for _ in range(steps):
                for j in range(8):
                    for pin in range(4):
                        self.coilPins[pin].value(self.seq[j][pin])
                    time.sleep_ms(2)

        self.angle = (self.angle + angle) % 360 if direction == 1 else (self.angle - angle) % 360

    def moveTo(self, angle):
        diff = angle - self.angle
        direction = 1 if diff > 0 else 0
        self.step(abs(diff), direction)

    def release(self):
        for pin in self.coilPins:
            pin.value(0)

And here is the code for the machine. This is a chatgpt generated code, which was corrected several time as I noticed diferent problems arose.

Prompts: how do I go from this to a step mottor from the math version above.
Want MicroPython stepper control code too? => sure. on the code above why do you have only 4 pins for the motors given that there is two motors?
the code you gave me for moving the step motors I think they move one motor at the time. etc.

import math
import time
from stepper import StepMotor

xy = []
with open('gcode_data.csv', 'r') as f:
    lines = f.readlines()

# Skip the header
for line in lines[1:]:
    parts = line.strip().split(',')
    if len(parts) == 3:
        x_val = float(parts[1])
        y_val = float(parts[2])
        xy.append((x_val, y_val))
        
xy=xy[::5]

# === CONFIGURATION ===
MOTOR_DISTANCE = 380.0  # distance between motors in mm
PULLEY_DIAMETER = 36.0  # pulley size in mm
PULLEY_CIRC = math.pi * PULLEY_DIAMETER
STEPS_PER_REV = 4096/8  # for 28BYJ-48 in half-step mode
MM_PER_REV = PULLEY_CIRC
DEGREES_PER_MM = 360.0 / MM_PER_REV

# === INITIALIZE MOTORS ===
motor1 = StepMotor([1, 2, 3, 4])   # GPIOs for Motor 1
motor2 = StepMotor([44, 7, 8, 9])  # GPIOs for Motor 2

def cartesian_to_lengths(x, y):
    l1 = math.sqrt(x**2 + y**2)
    l2 = math.sqrt((MOTOR_DISTANCE - x)**2 + y**2)
    return l1, l2

def move_to(x_target, y_target, current_x, current_y):
    global L1_current, L2_current

    # Convert target Cartesian coordinates to lengths
    L1_new, L2_new = cartesian_to_lengths(x_target, y_target)

    # Calculate the change in lengths
    delta_L1 = L1_new - L1_current
    delta_L2 = L2_new - L2_current

    # Convert length changes to angles
    angle1 = delta_L1 * DEGREES_PER_MM
    angle2 = delta_L2 * DEGREES_PER_MM

    # Determine direction: 1 for forward, 0 for backward
    dir1 = 0 if angle1 >= 1 else 0
    dir2 = 0 if angle2 >= 1 else 0

    # Move motors
    motor1.step(abs(angle1), dir1)
    motor2.step(abs(angle2), dir2)

    # Update current lengths
    L1_current = L1_new
    L2_current = L2_new

    return L1_new, L2_new, angle1, angle2, dir1, dir2

# === STARTING POSITION ===
current_x = 100
current_y = 100
L1_current, L2_current = cartesian_to_lengths(current_x, current_y)

# === PATH TO DRAW ===
path = xy

for x, y in path:
    L1_current, L2_current, angle1, angle2, dir1, dir2 = move_to(x, y, current_x, current_y)
    current_x, current_y = x, y
    time.sleep(0.5)

# Optional: release motors
motor1.release()
motor2.release()

Below you can find a a video of the machine working.