CPC Creation, Optimisation
Paragraphs 1 and 2 describe how I chose the key parameters for my parabola, however this optimisation was carried out using 22 and 66 cm exit apertures. I have included this here for completeness.
A revised and clearer process is described in paragraph 3, which is the process to follow for any future experiments.
1. Gemini Conversations
I have had issues retrieving such prompt histories so I asked Gemini to give me a prompt that will create scripts for the required steps, which is given in the callout below:
"Hello! I need your help to generate Python scripts and provide instructions for designing and modeling a 2D Compound Parabolic Concentrator (CPC) frame intended for laser cutting and press-fit assembly.
Overall Goal:
Create a 3D model of a CPC frame. The frame will consist of 15 radially arranged parabolic "legs" (ribs) and 4 circular "ring" supports at specific heights. The legs and rings will have features for press-fit assembly. The final design should be suitable for later processing to generate 2D cutting patterns for a laser cutter.
Part 1: Standalone Python Script for Generating Truncated CPC Profiles
Please generate a Python script (let's call it generate_cpc_profiles.py) with the following specifications:
Inputs for the entire script (user-configurable at the top):
D_exit_cm: Exit aperture diameter in centimeters (e.g., 66.0 cm).
acceptance_angles_deg_list: A list of acceptance half-angles in degrees for which to generate profiles (e.g., [15.0, 16.0, 17.0, 18.0, 19.0, 20.0]).
max_profile_height_m: A fixed maximum height in meters for all output profiles (e.g., 1.0 m). Profiles longer than this will be truncated.
num_points_profile: Number of points for generating the initial full profiles (e.g., 300).
output_txt_directory: Name of the directory to save text files (e.g., "cpc_profiles_truncated_txt").
output_png_directory: Name of the directory to save PNG plot files (e.g., "cpc_profiles_truncated_png").
Required Python Functions within the script:
generate_ideal_2d_cpc_profile(D_exit_m, theta_a_deg, num_points):
Purpose: Generates coordinates for a Welford & Winston (1989) / Winston, Miñano, Benítez (2005, Ch.2) style ideal 2D CPC profile.
This function should transform the profile to start at (r_e, 0) with the z-axis (height) increasing.
Outputs: (r_coords, z_coords, H_full_calculated, r_entry_calculated).
generate_true_full_2d_cpc(D_exit_m, theta_a_deg, num_points):
Purpose: Generates a full, non-truncated 2D CPC profile that achieves the theoretical maximum geometric concentration (Cg = 1/sin(theta_a)).
It should use generate_ideal_2d_cpc_profile as a base and anisotropically scale it to the correct theoretical full height (H_target_full = (r_e_m / sin(theta_a_rad)) * (cos(theta_a_rad) / sin(theta_a_rad)) * (1 + sin(theta_a_rad))) and entry radius (R_entry_target_full = r_e_m / sin(theta_a_rad)).
Outputs: (r_scaled, z_scaled, H_final_scaled, r_entry_final_scaled, Cg_theoretical_max).
truncate_profile_at_height(r_full, z_full, target_h_trunc):
Purpose: Truncates a given full profile (r_full, z_full) to a specified target_h_trunc.
Should handle edge cases (target height <=0, target height >= full height) and use linear interpolation for points between existing coordinates.
Outputs: (r_truncated, z_truncated, actual_h_truncated, r_entry_truncated).
save_profile_to_detailed_textfile(...):
Purpose: Saves profile data and key dimensions (including theoretical full height, theoretical Cg, whether it was truncated, target truncation height, actual output height, entry diameter, and calculated Cg of the output profile) to a formatted text file. The file should primarily contain the final r, z coordinates (in meters) suitable for later import.
Main Script Execution Logic (if
name
== "
main
":)
Create output directories if they don't exist.
Loop through each theta_a_deg in acceptance_angles_deg_list.
For each angle:
Call generate_true_full_2d_cpc to get the theoretical full profile.
Determine the effective_target_h_trunc_m for this profile: it's the minimum of max_profile_height_m (from script inputs) and the H_final_scaled of the true full profile. (Ensure this target is not less than a very small positive value if max_profile_height_m is <=0).
Call truncate_profile_at_height using the true full profile and effective_target_h_trunc_m to get the final output coordinates (r_output, z_output) and actual height (H_output).
Calculate the entry diameter and Cg for this H_output.
Save the r_output, z_output coordinates and all relevant metadata (as per save_profile_to_detailed_textfile) to a uniquely named .txt file (e.g., including D_exit, theta, and max height in the filename).
Generate a PNG plot showing the output profile (e.g., in red) and, if it was truncated, also show the outline of the true_full profile (e.g., in gray dashes) for comparison. Save to a unique PNG filename.
Part 2: Blender Python Script for Importing Profile and Initial 3D Construction
Please generate a Python script to be run inside Blender with the following specifications:
User-configurable Parameters at the top of the Blender script:
coordinate_file_path: Full, absolute path to one specific .txt coordinate file generated by the script in Part 1 (e.g., the one for theta=18 degrees, truncated at 1.0m).
object_base_name: Base name for objects created in Blender (e.g., "CPC_Frame").
num_legs: Number of parabolic legs (e.g., 15).
leg_material_thickness_m: Material thickness for legs (e.g., 0.005 for 5mm).
leg_depth_m: Desired depth (radial width) of the legs (e.g., 0.03 for 30mm).
ring_heights_m_list: A list of Z heights in meters for the circular rings (e.g., [0.0, 0.33, 0.66, 0.99]).
ring_radial_width_m: The desired radial width of the ring supports (this should be equal to leg_depth_m as per the design requirement, e.g., 0.03).
ring_material_thickness_m: Material thickness for rings (e.g., 0.005).
Blender Script Functionality:
load_rz_coordinates(filepath): Loads r, z coordinates from the specified text file.
create_2d_profile_line(r_coords, z_coords, obj_name, scale): Creates a Blender mesh object (vertices and edges) from the r,z coordinates, placing it in Blender's XZ plane (Blender X = r, Blender Z = z, Blender Y = 0). This will be the "master 2D leg profile."
create_rectangular_bevel_profile(width, height, profile_name): Creates a separate curve object representing a rectangle (e.g., width = leg_depth_m, height = leg_material_thickness_m). This will be used as a bevel object. Ensure its origin is centered.
Main Logic:
Load coordinates and create the master_2D_leg_profile object.
Convert master_2D_leg_profile to a Curve object.
Create the rectangular bevel profile object (e.g., leg_depth_m x leg_material_thickness_m).
Apply this bevel object to the master_2D_leg_profile curve to create one 3D leg (Single_3D_Leg). Ensure correct orientation of the bevel (30mm depth, 5mm thickness). The 30mm depth should be generally perpendicular to the CPC's central axis and following the curve, while the 5mm thickness is perpendicular to that.
Create an Empty at the world origin (CPC_Rotation_Pivot).
Use an Array Modifier on Single_3D_Leg with Object Offset pointing to CPC_Rotation_Pivot. Set Count to num_legs.
Rotate CPC_Rotation_Pivot around the Z-axis by 360 / num_legs degrees to arrange the legs.
(Initial Ring Creation - simple toruses or circles for now): For each height in ring_heights_m_list:
Determine the radius of the CPC at that specific Z height (either by reading from the coordinate file if possible, or by finding the corresponding X-value on the master_2D_leg_profile at that Z-height if the leg passes through the origin, or by measuring the radial position of the arrayed legs at that Z height).
Create a simple Torus object (or a Circle mesh) at that Z height with the determined Major Radius. For Torus, Minor Radius can be ring_radial_width_m / 2, and its tube cross-section can be made somewhat rectangular by adjusting Major/Minor Segments if needed (though a proper rectangular cross-section ring is more complex initially). For a Circle mesh, its radius will be the determined Major Radius.
This initial ring creation can be basic; the detailed press-fit features will be a manual modeling step later described in the instructions.
Part 3: Instructions for Blender and Fusion 360 (to be provided as text by the LLM)
Please provide clear, step-by-step instructions for a user, assuming they have the Blender script from Part 2:
Blender - Basic Frame Construction:
How to run the Blender Python script.
How to verify the initial 3D leg and array of legs are correct.
How to refine the simple rings created by the script into proper rectangular cross-section rings (ring_radial_width_m wide and ring_material_thickness_m thick). (Suggest using a similar "Bevel Object" method as used for the legs, by creating a separate rectangular profile for the rings).
How to ensure rings are at the correct Z heights and have the correct diameters to meet the legs.
Blender - Creating Press-Fit Notches (Conceptual):
Goal: At each intersection of a leg and a ring, the leg should have a notch cut into it, and the ring should have a corresponding slot. The leg's width at the notch should reduce by half (i.e., the notch depth into the leg is leg_material_thickness_m / 2). The slot in the ring should accommodate this reduced-width section of the leg.
Describe the general manual modeling process in Blender to create these notches/slots using Boolean modifiers (Difference) on individual, finalized leg and ring parts.
Example for one leg/ring intersection:
Create a "cutter" cube for the slot in the ring (sized appropriately for the leg's notched section).
Create a "cutter" object for the notch in the leg (sized ring_material_thickness_m deep into the leg, and leg_depth_m wide, and leg_material_thickness_m / 2 from each side face of the leg).
Emphasize applying modifiers and working on duplicates if necessary.
Mention the importance of checking normals and non-manifold geometry.
Blender - Preparing for Export to Fusion 360 (or for Laser Cutting from Blender):
How to ensure each unique leg and unique ring is a separate, "clean" 3D object.
How to "flatten" or get the 2D cutting profiles:
Rings: Exporting a top-down orthographic view as DXF/SVG.
Legs (Parabolic Ribs): Explain that this is the trickiest. Suggest the method of taking the original 2D master parabolic profile line (from the imported coordinates, before 3D beveling), and in a 2D environment (either Blender's 2D tools, or after exporting this line to other software), offsetting it to create the 30mm depth, then closing the ends to form the 2D rib shape.
Recommended export formats from Blender (DXF, SVG).
Briefly mention unit consistency.
Fusion 360 - Post-Processing (Conceptual):
How to import the DXF/SVG files into Fusion 360.
Verifying dimensions and scale.
Using the "Extrude" command in Fusion 360 on the 2D sketches to recreate the 5mm thick parts (this helps verify the 2D patterns).
Arranging parts on a sheet for laser cutting (nesting) – typically done in CAM software, but Fusion has some capabilities.
Mentioning kerf adjustment as a final step, usually done in CAM software or by offsetting paths in Fusion/CAD.
Important Notes for the LLM:
The user has 5mm material thickness for all parts.
The "depth" of the leg (30mm) should be equal to the "radial width" of the rings (30mm).
The press-fit notch in the leg means the leg becomes thinner (leg_material_thickness_m / 2 on each side, so effectively it might pass through a slot in the ring that is leg_material_thickness_m wide if the notches are on both sides, or the leg is made thinner in one direction). Clarify that the slot in the ring should be leg_material_thickness_m wide (to accept the 5mm thick leg material after it has been notched) and leg_depth_m long (to match the leg's depth). The notch in the leg should be ring_material_thickness_m "deep" (removing material from the 30mm depth of the leg) where it passes through the ring.
Of course it is never plain sailing, the next prompt is :
Concerning Part 1, i'm not getting a CPC with a varying r, it stays constant at 0.33m. So there is something wrong. If you could use Chapter 5 from Nonimaging Optics. (Roland Winston, Juan C. Minano etc.) along with appendix G, H, I
In order to determine a CPC profile applying the edge-ray principle discussed in Nonimaging Optics [1], we should first understand:
- Edge-Ray Principle: The fundamental design principle for a CPC is that all rays entering the aperture at the maximum acceptance half-angle (these are the "extreme rays") should, after one reflection (or no reflection if they pass directly), be directed to the edge of the exit aperture (the absorber). See Figure CPC1.
- Parabolic Shape: To achieve this for the right-hand wall of the CPC (for r > 0):
- The extreme rays incident from the left at + (relative to the CPC's optical axis) must be reflected towards the right edge of the exit aperture, which is at ( , 0).
- The parabolic reflector shape that achieves this has its focus at the opposite edge of the exit aperture, i.e., at (-, 0).
- The axis of this parabola is tilted by the acceptance angle with respect to the CPC's main optical axis (the z-axis).
- String Method Visualization (Chapter 2, Fig 2.4 of "Nonimaging Optics"):
- The string method provides a way to trace out such a profile. Imagine a string of fixed length. One end is anchored at the focus (-, 0). The other end is "attached" to a line representing the wavefront of the extreme rays (a line tilted at passing through the edge of the entry aperture). The CPC profile is the locus of points where the string is taut when a segment of it is aligned with the extreme ray.
- The mathematical derivation leads to the parabolic shape described.
The generate_ideal_2d_cpc_profile function in the script below builds the parabola by:
- Defining its focus implicitly by its properties related to r_e () and (theta_a).
- Calculating its semi-latus rectum p.
- Using the polar equation of a parabola rho = p / (1 - cos(u)) where u is the angle relative to the parabola's own axis.
- Rotating and translating these coordinates to the CPC's frame, ensuring the profile starts at (r_e, 0).
the CPCs for acceptance angles 15-20 degrees for an exit aperture of 66 cm, truncated at 1m.
1.1 CPC plots
This produces the CPC profiles in text files and visualises them in png files, an example of both are given for 18 degrees below:
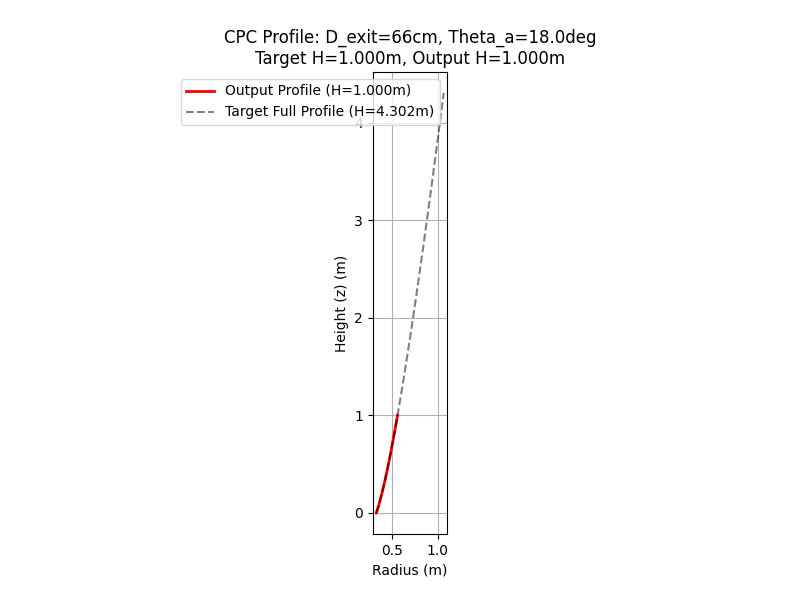
1.2 CPC Optimisation
Now that I can correctly generate CPCs at different acceptance angles and for different exit apertures, it’s time to choose an acceptance angle to be used for the solar cooker. Here I will compare the concentration coeffecient for different and :
Could you also add a script to compare the different Cg for the different acceptance angles 13, 15, 18 and 20 degrees at 40 - 100% height truncation in 10% intervals, including the theoretical C_g for full cpcs, and include the height of each acceptance angle cpc at 100% height
Can we correlate C_g with total solar power or energy at the exit aperture ?
I’m analysing the CPC properties for an exit aperture of 0.66m consistent with the intended oven / cooking plate size even though the initial proof of concept experiment will be with a 22cm pan.
# CPC_energy.py (or analyze_cpc_power.py)
import numpy as np
import os
import datetime # For timestamp in filename
# --- Option 1: Attempt to import from CPC_generation ---
# This is preferred if CPC_generation.py is in the same directory or your PYTHONPATH
try:
from CPC_generation import (
generate_true_full_2d_cpc,
truncate_profile_at_height,
# Assuming these constants are available in CPC_generation.py
# If not, define them locally below
CM_TO_M, M_TO_CM, EPSILON
)
print("Successfully imported functions from CPC_generation.py")
except ImportError:
print("Could not import from CPC_generation.py. Using local definitions.")
print("Ensure the function definitions in the fallback section are up-to-date.")
# --- Fallback: Define necessary constants and functions locally ---
CM_TO_M = 0.01
M_TO_CM = 100
EPSILON = 1e-9 # A small number
# Placeholder for functions - REPLACE with actual definitions from CPC_generation.py
# if import fails and you use this fallback.
def generate_ideal_2d_cpc_profile(D_exit_m, theta_a_deg, num_points):
# ... (Full definition from your CPC_generation.py)
# For brevity, this is just a placeholder. You need the actual code here.
print("Warning: Using placeholder for generate_ideal_2d_cpc_profile")
r_e_m = D_exit_m / 2.0
return np.array([r_e_m, r_e_m]), np.array([0,0.1]), 0.1, r_e_m
def generate_true_full_2d_cpc(D_exit_m, theta_a_deg, num_points):
# ... (Full definition from your CPC_generation.py)
print("Warning: Using placeholder for generate_true_full_2d_cpc")
r_e_m = D_exit_m / 2.0
H_theo_full = 1.0 # Placeholder
R_entry_theo_full = r_e_m * (1/np.sin(np.deg2rad(theta_a_deg)) if np.sin(np.deg2rad(theta_a_deg)) > EPSILON else 1)
Cg_2D_theo_max = R_entry_theo_full / r_e_m if r_e_m > EPSILON else 1
return np.array([r_e_m, R_entry_theo_full]), np.array([0, H_theo_full]), H_theo_full, R_entry_theo_full, Cg_2D_theo_max
def truncate_profile_at_height(r_full, z_full, target_h_trunc):
# ... (Full definition from your CPC_generation.py)
print("Warning: Using placeholder for truncate_profile_at_height")
if len(r_full) == 0: return np.array([]), np.array([]), 0.0, 0.0
return r_full, z_full, z_full[-1], r_full[-1] # Simplified placeholder
# --- End Fallback ---
# --- Analysis Script Inputs ---
D_EXIT_CM_ANALYSIS = 66.0
ANALYSIS_ACCEPTANCE_ANGLES_DEG = [13.0, 15.0, 18.0, 20.0]
ANALYSIS_TRUNCATION_PERCENTAGES = [40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0]
NUM_POINTS_PROFILE_ANALYSIS = 300
SOLAR_IRRADIANCE_W_PER_M2 = 1000.0
OPTICAL_EFFICIENCY_FRACTION = 0.80
TIME_DURATION_HOURS = 1.0
# --- Output File Configuration ---
OUTPUT_RESULTS_FILENAME_BASE = "cpc_power_analysis_results"
OUTPUT_DIRECTORY = "analysis_results" # Optional: specify a subdirectory
# ---
def run_cpc_power_analysis():
D_exit_m = D_EXIT_CM_ANALYSIS * CM_TO_M
r_e_m = D_exit_m / 2.0
A_exit_m2 = np.pi * (r_e_m**2)
# --- Prepare for file output ---
if OUTPUT_DIRECTORY and not os.path.exists(OUTPUT_DIRECTORY):
os.makedirs(OUTPUT_DIRECTORY)
timestamp = datetime.datetime.now().strftime("%Y%m%d_%H%M%S")
output_filename = f"{OUTPUT_RESULTS_FILENAME_BASE}_{timestamp}.txt"
if OUTPUT_DIRECTORY:
output_filepath = os.path.join(OUTPUT_DIRECTORY, output_filename)
else:
output_filepath = output_filename
output_lines = [] # Store lines to write to file
# --- Header Information ---
header_info = []
header_info.append(f"CPC Power/Energy Analysis Report")
header_info.append(f"Date: {datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')}")
header_info.append(f"Input D_exit: {D_EXIT_CM_ANALYSIS:.1f} cm (A_exit = {A_exit_m2:.4f} m^2)")
header_info.append(f"Solar Irradiance (I_solar): {SOLAR_IRRADIANCE_W_PER_M2:.1f} W/m^2")
header_info.append(f"Optical Efficiency (eta_opt): {OPTICAL_EFFICIENCY_FRACTION*100:.1f}%")
header_info.append(f"Time Duration for Energy: {TIME_DURATION_HOURS:.1f} hours")
header_info.append("=" * 120)
for line in header_info:
print(line)
output_lines.append(line)
table_header_format = (f"{'Theta_a':<9} | {'Full H':<8} | {'Cg2D_theo':<9} | {'Cg3D_theo':<9} | "
f"{'Trunc %':<7} | {'H_trunc':<9} | {'R_entry':<9} | {'Cg2D_tr':<9} | {'Cg3D_tr':<9} | "
f"{'P_exit(W)':<10} | {'E_exit(Wh)':<11}")
print(table_header_format)
output_lines.append(table_header_format)
print("-" * len(table_header_format))
output_lines.append("-" * len(table_header_format))
analysis_results_summary = [] # For potential plotting later
for theta_a_deg in ANALYSIS_ACCEPTANCE_ANGLES_DEG:
try:
r_full_profile, z_full_profile, H_theo_full, R_entry_theo_full, Cg_2D_theo_max = \
generate_true_full_2d_cpc(D_exit_m, theta_a_deg, NUM_POINTS_PROFILE_ANALYSIS)
except Exception as e:
error_msg = f"Error generating full profile for Theta_a={theta_a_deg}: {e}"
print(error_msg)
output_lines.append(error_msg)
print(f"{theta_a_deg:<9.1f} | {'ERROR generating full profile':<100}")
output_lines.append(f"{theta_a_deg:<9.1f} | {'ERROR generating full profile':<100}")
continue
if len(r_full_profile) < 2:
fail_msg = f"{theta_a_deg:<9.1f} | {'N/A':<8} | ... (Full profile generation failed or returned degenerate)"
print(fail_msg)
output_lines.append(fail_msg)
continue
Cg_3D_theo_max = Cg_2D_theo_max**2 if Cg_2D_theo_max >=0 else 0
full_cpc_data = { # For plotting
"theta_a": theta_a_deg, "H_full_m": H_theo_full,
"Cg_2D_theoretical_max": Cg_2D_theo_max, "Cg_3D_theoretical_max": Cg_3D_theo_max,
"truncations": []
}
line_full_theo = (f"{theta_a_deg:<9.1f} | {H_theo_full:<8.3f} | {Cg_2D_theo_max:<9.3f} | {Cg_3D_theo_max:<9.3f} | "
f"{'(Full)':<7} | {'-':<9} | {'-':<9} | {'-':<9} | {'-':<9} | "
f"{'-':<10} | {'-':<11}")
print(line_full_theo)
output_lines.append(line_full_theo)
for trunc_perc in ANALYSIS_TRUNCATION_PERCENTAGES:
effective_target_h_trunc_m = H_theo_full * (trunc_perc / 100.0)
if H_theo_full > EPSILON: # Avoid negative or tiny target height if H_theo_full is already tiny
effective_target_h_trunc_m = max(EPSILON, effective_target_h_trunc_m)
else: # If full height is essentially zero (e.g. theta_a=90), truncated height is also zero
effective_target_h_trunc_m = 0.0
R_entry_output_m = 0.0 # Default for failed truncation
H_output = 0.0 # Default
status_msg_part = f"{H_output:<9.3f}" # Default status
try:
r_output, z_output, H_output_calc, R_entry_output_m_calc = \
truncate_profile_at_height(r_full_profile, z_full_profile, effective_target_h_trunc_m)
H_output = H_output_calc
R_entry_output_m = R_entry_output_m_calc
status_msg_part = f"{H_output:<9.3f}"
except Exception as e:
error_msg_trunc = f"Error during truncation for Theta_a={theta_a_deg}, Trunc%={trunc_perc}: {e}"
print(error_msg_trunc)
output_lines.append(error_msg_trunc)
status_msg_part = "ERROR" # Indicate error in table
P_exit_W = 0.0
E_exit_Wh = 0.0
Cg_2D_output = 0.0
Cg_3D_output = 0.0
if status_msg_part != "ERROR" and ( (len(r_output) == 0 if 'r_output' in locals() else True) or r_e_m < EPSILON):
status_msg_part = "N/A (empty)" if 'r_output' in locals() and len(r_output) == 0 else status_msg_part
elif status_msg_part != "ERROR":
Cg_2D_output = R_entry_output_m / r_e_m
Cg_3D_output = Cg_2D_output**2
A_entry_output_m2 = np.pi * (R_entry_output_m**2)
P_exit_W = SOLAR_IRRADIANCE_W_PER_M2 * A_entry_output_m2 * OPTICAL_EFFICIENCY_FRACTION
E_exit_Wh = P_exit_W * TIME_DURATION_HOURS
data_line = (f"{'':<9} | {'':<8} | {'':<9} | {'':<9} | "
f"{trunc_perc:<7.1f} | {status_msg_part:<9} | {R_entry_output_m:<9.4f} | {Cg_2D_output:<9.3f} | {Cg_3D_output:<9.3f} | "
f"{P_exit_W:<10.2f} | {E_exit_Wh:<11.2f}")
print(data_line)
output_lines.append(data_line)
full_cpc_data["truncations"].append({
"percentage": trunc_perc, "H_trunc_m": H_output, "R_entry_trunc_m": R_entry_output_m,
"Cg_2D_trunc": Cg_2D_output, "Cg_3D_trunc": Cg_3D_output,
"P_exit_W": P_exit_W, "E_exit_Wh": E_exit_Wh
})
analysis_results_summary.append(full_cpc_data)
separator_line = "-" * len(table_header_format)
print(separator_line)
output_lines.append(separator_line)
end_marker = "=" * 120
print(end_marker)
output_lines.append(end_marker)
# --- Write to file ---
try:
with open(output_filepath, 'w') as f:
for line in output_lines:
f.write(line + "\n")
print(f"\nSuccessfully saved analysis results to: {output_filepath}")
except IOError as e:
print(f"\nError writing results to file {output_filepath}: {e}")
return analysis_results_summary
if __name__ == "__main__":
results_data = run_cpc_power_analysis() # This now also writes the file
# --- Plotting (optional, kept from before) ---
try:
import matplotlib.pyplot as plt
plotting_enabled = True
except ImportError:
plotting_enabled = False
print("\nMatplotlib not found. Skipping summary plot generation.")
if plotting_enabled and results_data:
# ... (Plotting code remains the same as in the previous version)
# For brevity, omitting the plotting code here, but it should work as before.
# Ensure you copy it from the previous response if needed.
fig, axes = plt.subplots(nrows=2, ncols=1, figsize=(14, 12), sharex=True)
markers = ['o', 's', '^', 'D', 'v', '<', '>']
for i, angle_data in enumerate(results_data):
theta_a = angle_data["theta_a"]
H_full = angle_data["H_full_m"]
Cg_3D_theo = angle_data["Cg_3D_theoretical_max"]
percentages = [t["percentage"] for t in angle_data["truncations"]]
cg_3d_values = [t["Cg_3D_trunc"] for t in angle_data["truncations"]]
p_exit_values = [t["P_exit_W"] for t in angle_data["truncations"]]
label = (f'$\\theta_a = {theta_a:.0f}^\\circ$ (H_f={H_full:.2f}m, Cg$_{{3D,theo}}$={Cg_3D_theo:.1f})')
axes[0].plot(percentages, cg_3d_values, marker=markers[i % len(markers)], linestyle='-', label=label)
axes[1].plot(percentages, p_exit_values, marker=markers[i % len(markers)], linestyle='--', label=label)
axes[0].set_ylabel("3D Geometric Concentration (Cg_3D)")
axes[0].set_title(f"CPC Performance vs. Truncation (D_exit = {D_EXIT_CM_ANALYSIS:.1f} cm, I_solar={SOLAR_IRRADIANCE_W_PER_M2} W/m$^2$, $\\eta_{{opt}}$={OPTICAL_EFFICIENCY_FRACTION:.2f})")
axes[0].grid(True, which='both', linestyle=':')
axes[0].legend(title="Acceptance Angle", bbox_to_anchor=(1.03, 1), loc='upper left', fontsize='small')
axes[1].set_xlabel("Truncation of Full Height (%)")
axes[1].set_ylabel(f"Power at Exit, P_exit (W)")
axes[1].grid(True, which='both', linestyle=':')
plt.xticks(ANALYSIS_TRUNCATION_PERCENTAGES)
fig.tight_layout(rect=[0, 0, 0.85, 1])
# --- Filename for plot ---
plot_timestamp = datetime.datetime.now().strftime("%Y%m%d_%H%M%S")
plot_filename_base = "cpc_power_vs_truncation_plot"
plot_filename = f"{plot_filename_base}_{plot_timestamp}.png"
if OUTPUT_DIRECTORY:
plot_filepath = os.path.join(OUTPUT_DIRECTORY, plot_filename)
else:
plot_filepath = plot_filename
plt.savefig(plot_filepath, bbox_inches='tight')
print(f"\nSaved summary plot to: {plot_filepath}")
# plt.show()This produces a graph comparing CPC Geometric Concentration vs. Truncation Percentage, and also Power at Exit vs Truncation for a 66 cm exit aperture:
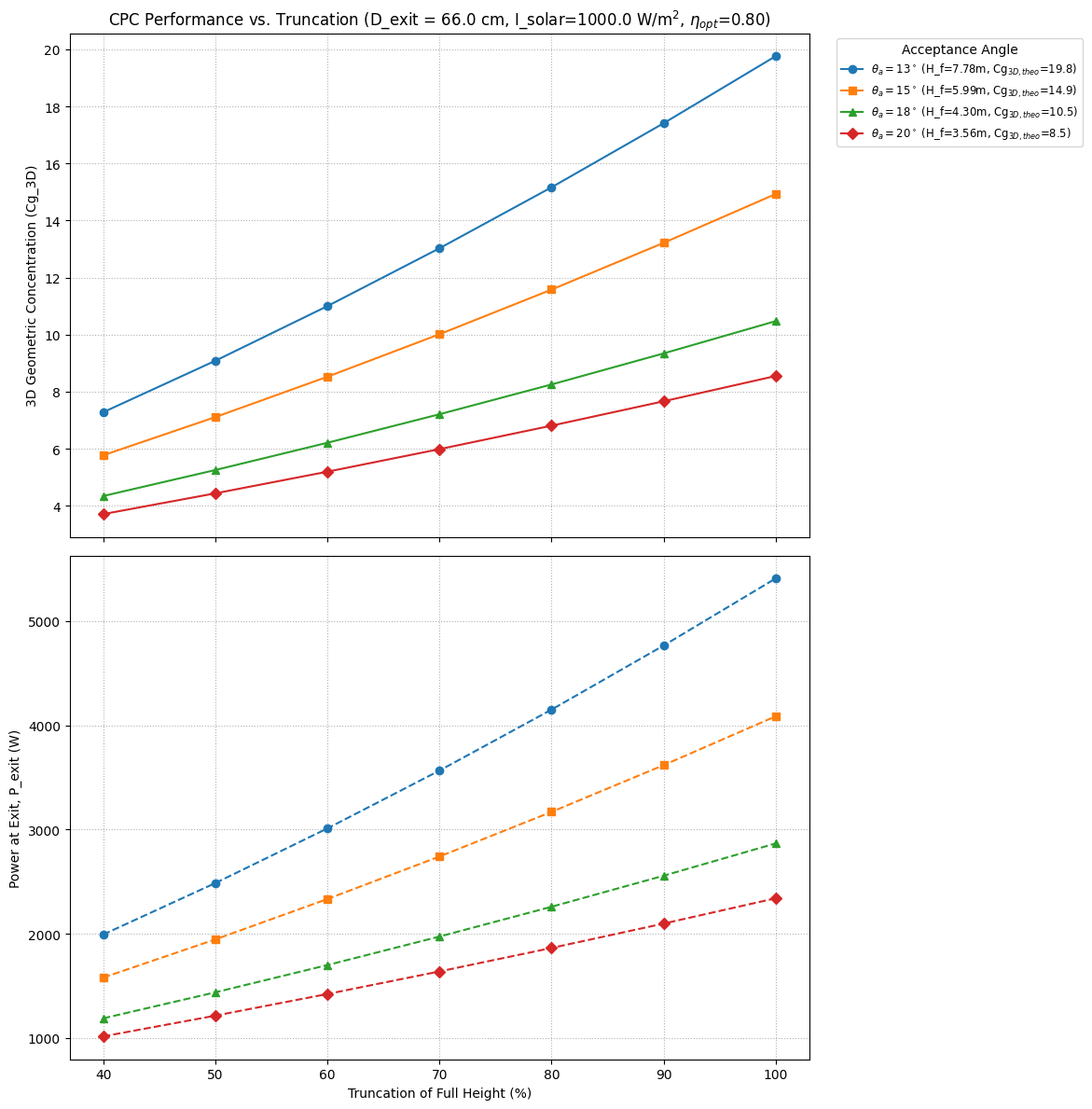
The simplified logic:
- How big is the CPC's mouth (entry aperture)? -> A_entry_output_m2
- How much sunlight hits this mouth? -> SOLAR_IRRADIANCE_W_PER_M2 * A_entry_output_m2
- How much of that sunlight actually gets through the CPC to the small end (exit aperture) after losses? -> Multiply by OPTICAL_EFFICIENCY_FRACTION. This gives P_exit_W.
- If this power is delivered for a certain number of hours, what's the total energy? -> Multiply P_exit_W by TIME_DURATION_HOURS. This gives E_exit_Wh.
1.3 Truncation
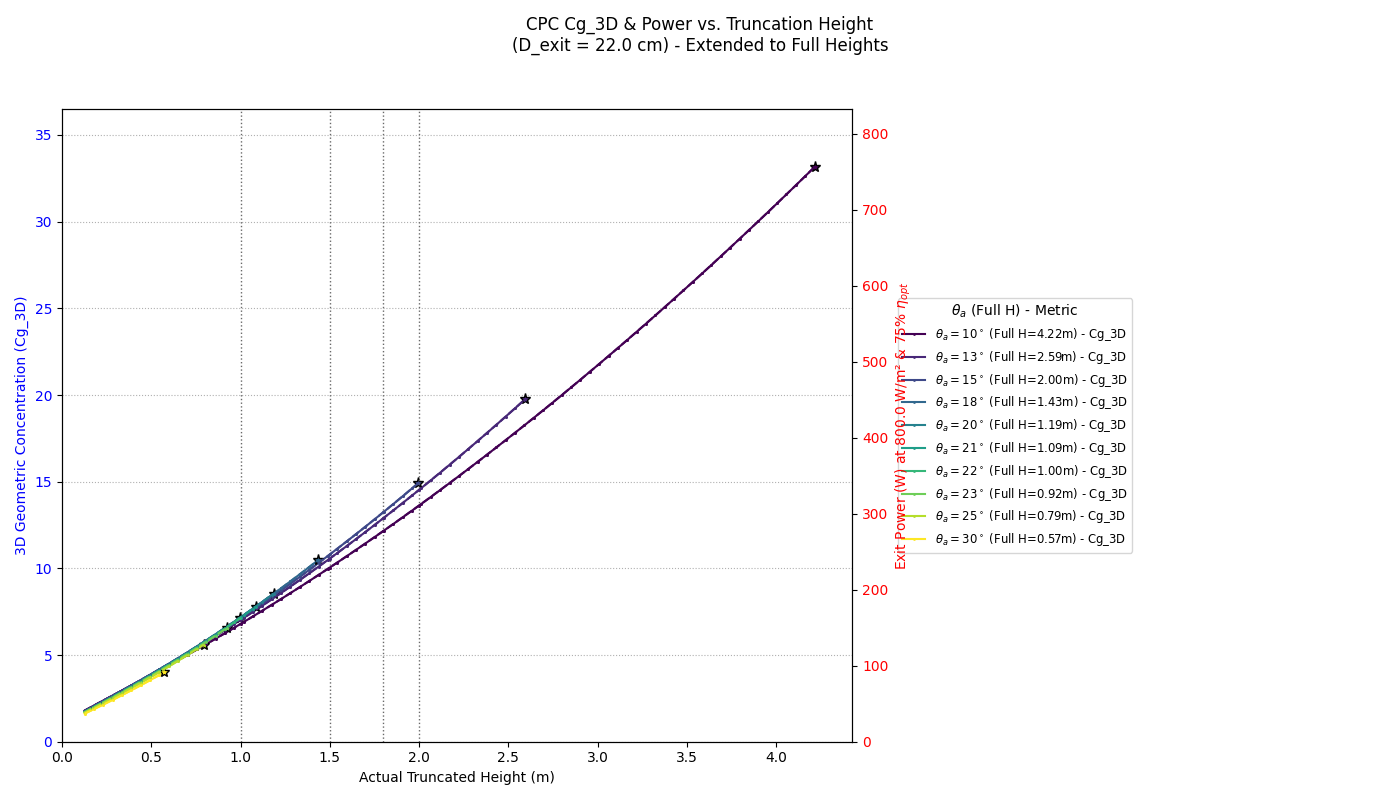
Now I would like to analyse different CPCs truncated at 1m and 2m for different acceptance angles. I am going to do a primary experiment with an exit aperture of 22 cm and then the final design with 66cm.
For both of these apertures I would like:
- a figure comparing the different CPC profiles
- a table in a text file comparing power with acceptance angle at 1 m and 2 m truncation. If you could include entry and exit aperture
- any other information you consider valuable in order to choose the acceptance angle and truncation height for my solar cooker
I'd also like to have a plot of the different power results for different truncations and acceptance angles so it is more visually apparant which cpc generates the most power at 1m, 1,5 and 1.8 m height.
I’d like a plot chart with a clear legend. The height should extend to full height, with a dynamic x axis and a comparison with power
We now have enough information to choose an appropriate for the experiment with a 22 cm pot placed at the exit aperture (=0.11 m).
| CPC Candidate Summary - 2025-05-27 13:56:38 | |||||||
|---|---|---|---|---|---|---|---|
| Solar Irradiance: 800.0 W/m^2 | Optical Eff: 0.75 | ||||||
| D_exit_cm | theta_a | H_target_m | H_actual_m | D_entry_cm | Cg_3D | P_exit_W | Notes |
| 22 | 10 | 0.95 | 0.95 | 56 | 6.49 | 148 | |
| 22 | 10 | 1 | 1 | 57.4 | 6.8 | 155 | |
| 22 | 10 | 1.05 | 1.05 | 58.6 | 7.11 | 162.1 | |
| 22 | 13 | 0.95 | 0.95 | 56.9 | 6.69 | 152.7 | |
| 22 | 13 | 1 | 1 | 58.3 | 7.02 | 160.2 | |
| 22 | 13 | 1.05 | 1.05 | 59.7 | 7.36 | 167.9 | |
| 22 | 15 | 0.95 | 0.95 | 57.3 | 6.78 | 154.5 | |
| 22 | 15 | 1 | 1 | 58.7 | 7.12 | 162.3 | |
| 22 | 15 | 1.05 | 1.05 | 60.1 | 7.47 | 170.3 | |
| 22 | 18 | 0.95 | 0.95 | 57.5 | 6.83 | 155.7 | |
| 22 | 18 | 1 | 1 | 58.9 | 7.18 | 163.7 | |
| 22 | 18 | 1.05 | 1.05 | 60.4 | 7.54 | 171.9 | |
| 22 | 20 | 0.95 | 0.95 | 57.4 | 6.82 | 155.5 | |
| 22 | 20 | 1 | 1 | 58.9 | 7.17 | 163.6 | |
| 22 | 20 | 1.05 | 1.05 | 60.4 | 7.54 | 171.9 | |
| 22 | 21 | 0.95 | 0.95 | 57.4 | 6.8 | 155.1 | |
| 22 | 21 | 1 | 1 | 58.9 | 7.16 | 163.2 | |
| 22 | 21 | 1.05 | 1.05 | 60.3 | 7.52 | 171.5 | |
| 22 | 22 | 0.95 | 0.95 | 57.3 | 6.78 | 154.5 | |
| 22 | 22 | 1 | 0.999 | 58.7 | 7.13 | 162.5 | TgtH(1.00)>FullH(1.00). |
2. Parameters to be used for the experiment
For the experiment I used an 18 degree and a of 1.0 m so that it is manageable. The expected Power generation is around 150 W assuming a solar irradiance with an optical efficiency of 0.75 for a 22cm exit aperture.
However, for the experiment I decided to use a 39cm exit aperture which significantly changes things. By the time I decided to revise this optimisation it was too late to change any of these parameters as the CPC was already built.
3. Revised Optimisation for future experiments and Clarification
3.1 Key Parameters
After the initial experiments, I went back to the optimisation process, in order to improve clarity in understanding for both myself and any future readers.
The key parameters to optimise are :
- Exit aperture
- Acceptance demi angle
- Truncation
For this project we are going to concentrate on parameters 2 and 3, maintaining a constant exit aperture of 39 cm. The exit aperture should be investigated further and is directly linked to the cooking pot/oven. For simplicity and not to waste time I chose to keep it constant.
3.2 Truncation and Exit aperture Optimisation
This optimisation process aims to determine an appropriate acceptance angle, and height of the CPC for a given exit aperture. The higher the acceptance angle, the wider entry aperture and the higher the CPC.
The following scripts compare acceptance half angles for a given exit aperture, estimating the estimated concentration coefficient and power output for
- different truncated heights (
cpc_performance_vs_truncation.py),
- for a 1m truncated height (
cpc_optimize_angle_at_fixed_truncation.py).
However, for this experiment the height is truncated at 1m for practical reasons. The exit aperture, acceptance angles, truncation percentages can be modified easily in the scripts:
# cpc_performance_vs_truncation.py
# --- User-configurable Inputs ---
D_EXIT_CM_ANALYSIS = 66.0 # Exit aperture diameter in centimeters
ANALYSIS_ACCEPTANCE_ANGLES_DEG = [12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0, 19.0, 20.0] # Acceptance half-angles
# Truncation from 20% to 100% of full height. 17 points means steps of 5% (e.g., 20, 25, ..., 100)
ANALYSIS_TRUNCATION_PERCENTAGES = np.linspace(20, 100, 17).tolist()
NUM_POINTS_PROFILE_ANALYSIS = 300 # Number of points for generating initial full CPC profiles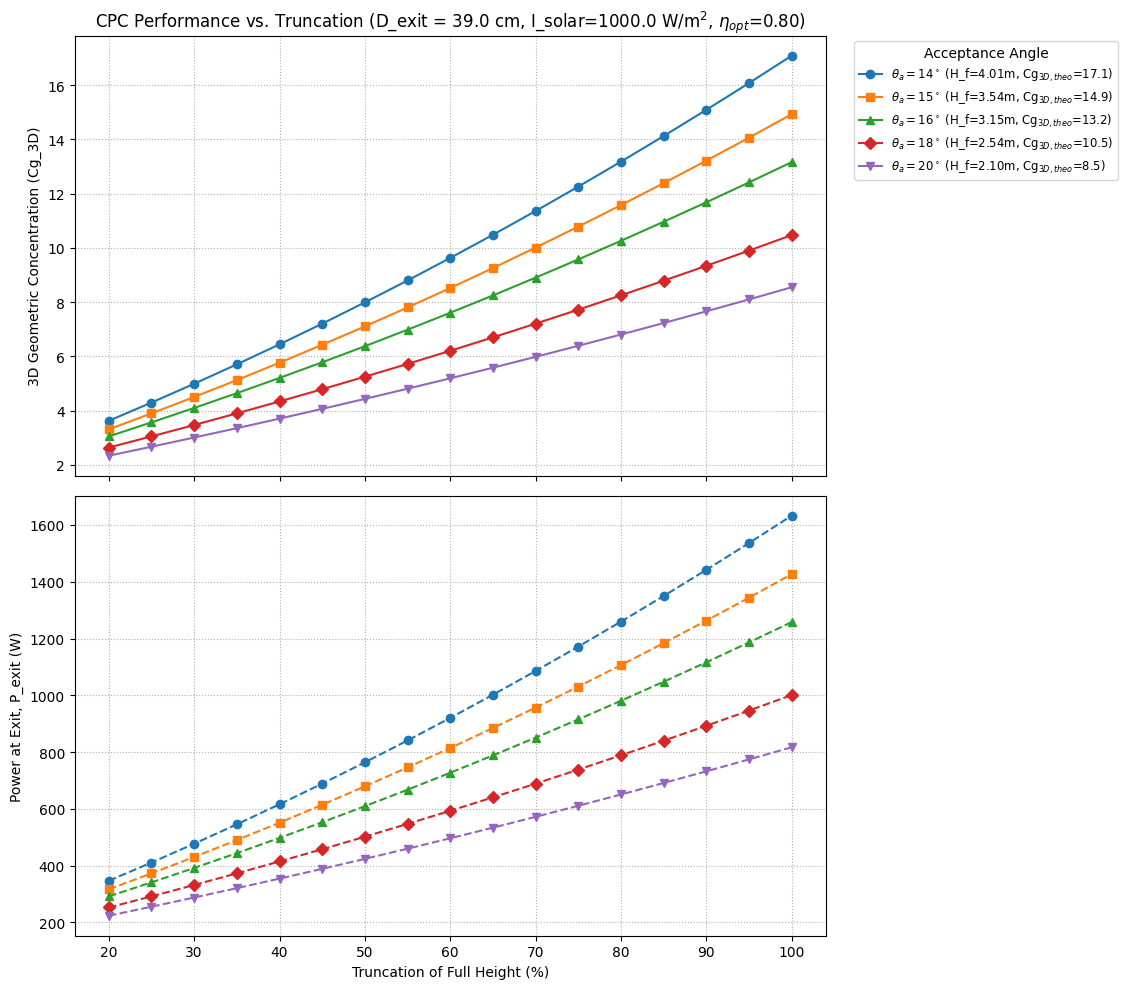
# cpc_optimize_angle_at_fixed_truncation.py
# --- User-configurable Inputs ---
D_EXIT_CM_ANALYSIS = 66.0 # Exit aperture diameter in centimeters
ANALYSIS_ACCEPTANCE_ANGLES_DEG = [12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0, 19.0, 20.0] # Acceptance half-angles to test
FIXED_TRUNCATION_HEIGHT_M = 1.0 # The fixed truncation height for the experiment
NUM_POINTS_PROFILE_ANALYSIS = 300 # Number of points for generating initial full CPC profiles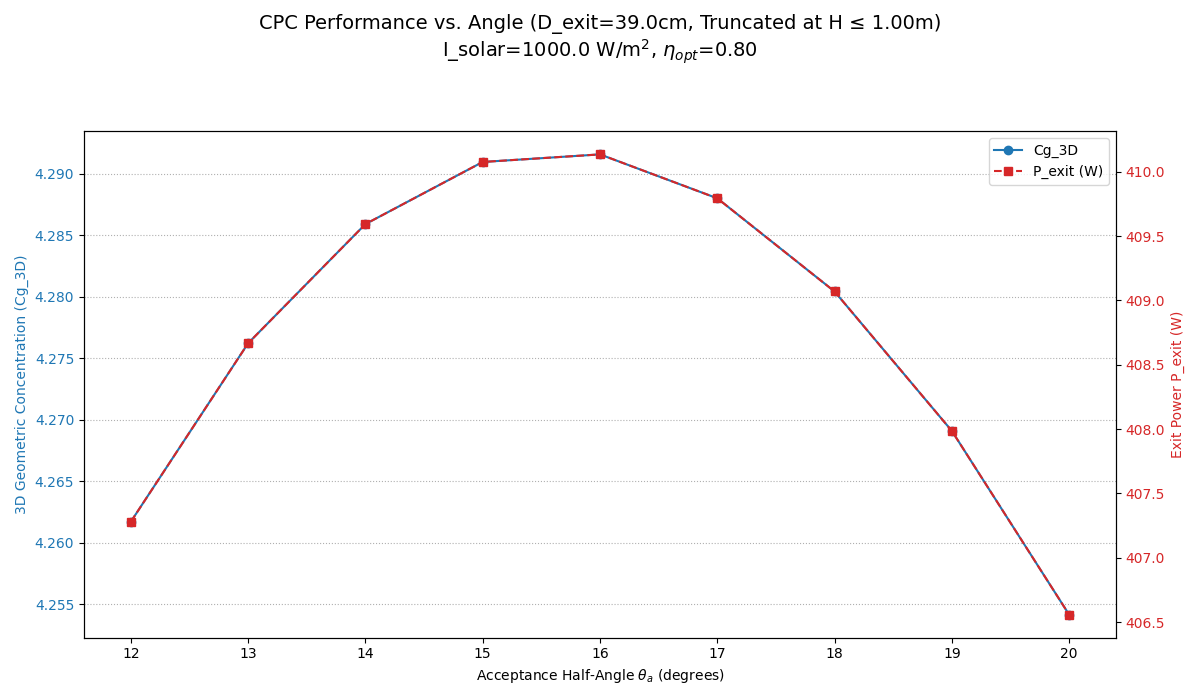
Based on this analysis an at 16 degrees would have been more appropriate than 18.