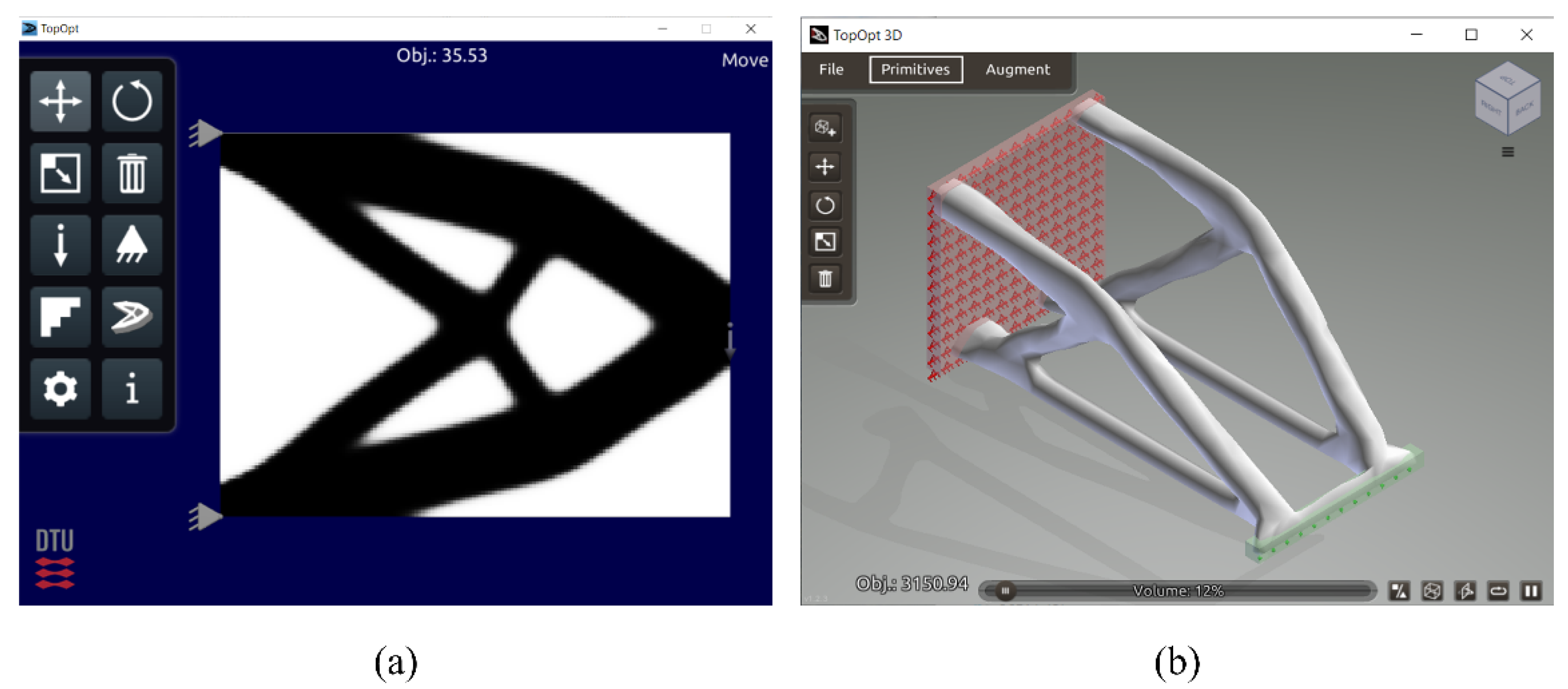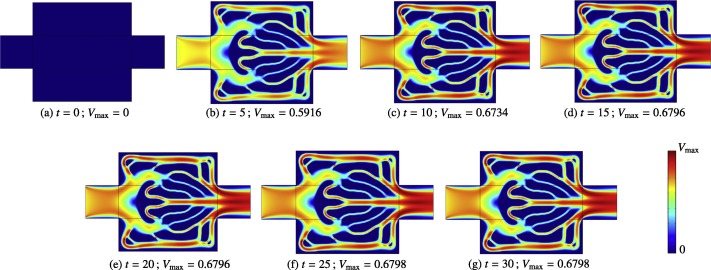



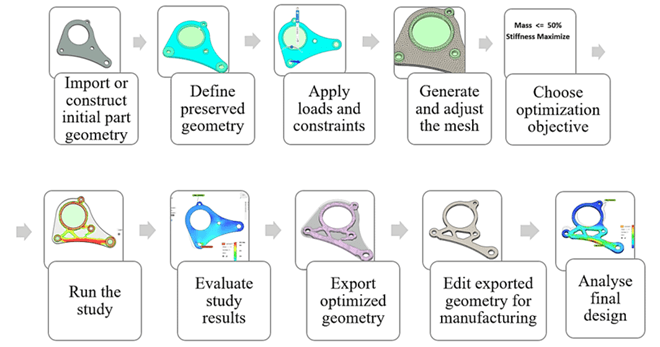

(*adapted from here)
A common topology optimization problem is compliance minimization, where we seek the "stiffest" structure within a certain volume limit to withhold a particular load:
$$ \min_{\bf x} \quad {\bf f} := {\bf d}^T {\bf K}({\bf x}) {\bf d} $$
$$ \text{subject to:} \quad {\bf h} := {\bf K}({\bf x}) {\bf d} = {\bf u}, $$
$$ \quad {\bf g} := V(\textbf{x}) \leq v,$$
$$ \textbf{x} \in [0,1]. $$
The structure under design is segmented into $n$ finite elements, and a density value $x_i$ is assigned to each element $i \in {1,2,...,n}$: A higher density corresponds to a less porous material element and higher Yong's modulus. Reducing the density to zero is equivalent to creating a hole in the structure. Thus, the set of densities ${\bf x}={x_i}$ can be used to represent the topology of the structure and is considered as the variables to be optimized.
${\bf d} \in \mathbb{R}^{n_d\times 1}$ is the displacement of the structure under the load ${\bf u}$, where $n_d$ is the degrees of freedom (DOF) of the system (i.e., the number of x- and y-coordinates of nodes from the finite element model of the structure)
${\bf K(x)}$ is the global stiffness matrix for the structure.