Digital Mechanical Materials

Group members: Pierre-Brice Bintein, Nicolas Decoster, Victor Levy, Denis Terwagne

FAB14 Workshop

The wildcard week group project served has a basis for a workshop that was given at the FAB14 Conference in Toulouse, France (scheduled event).

Here is the tutorial that was made for the conference:

• FAB14 Workshop: Digital Mechanical Material by Design, a physicist approach

Mechanical structure functions

The function of the mechanical metamaterial is given by the material and the geometrical structure.

Here is a youtube channel with a some metamaterials for inspiration :

Fabrication processes

There are different ways to fabricate mechanical metamaterials. Here are some examples.

Thermomorph

Thermorph from Morphing Matter Lab on Vimeo.

3D printing

Laser cutting

Part I: parametric Kirigami

In this part, we are going to make mechanical metamaterials from kirigami. Kirigami is simply a sheet folding in which there are cuts. When the 2D structure is stretched, it deforms in a particular way: It can expand, retract, rotate, move out of plane,...

Exloring these structures is really eased by digital fabrication. The design of these structure can be made parametrically which allow us to explore physically the complete space parameters. It's unleashing the power of numerical simulation to the physical world (this is a real revolution in how problems are tackled in Science).

After exploring the scientific literature on kirigami structures and mechanical meta materials (which is really recent), we found this nice work to start from.

Bistable Auxetic Mechanical Metamaterials Inspired by Ancient Geometric Motifs from Ahmad Rafsanjani on Vimeo.

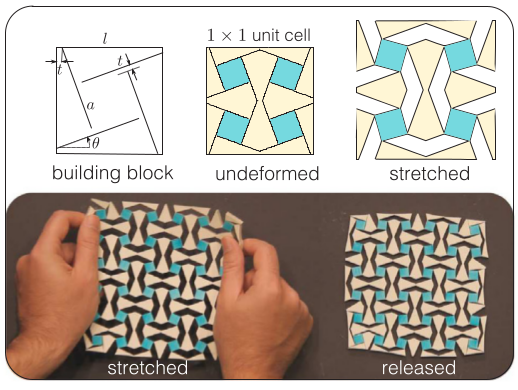
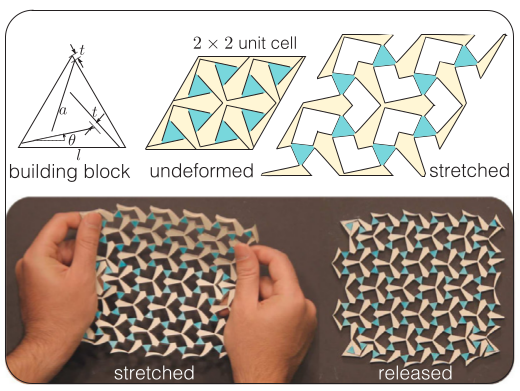
Bistable Auxetic Pattern Generator

Desired width
Desired height
Cell size
t
θ
Add border
Pattern type	Bistable auxetics Triangular auxetics
Note : you must update SVG before copy/download.

Part II: Molding and casting 2D Mechanical metamaterials

Mould design files F3D, DXF.

We worked on a way to make a 2D metamaterial that is made quickly and can be quickly modified.
Different solutions have been envisaged with Denis, Nicolas and Axel.

3D printing of a mold. Much too long to print: more than 4 hours . CNC: same problem .We tested soluble PVA. The idea is to print the negative of the form, to pour the resin and to dissolve the material after the drying of the resin. Tests have been done on the UP of Denis' lab and at Digiscope, inconclusive.
We worked on another idea. The idea was to find metal cylinders and arrange them on a plexiglass plate, laser cut. It is the fastest and most efficient technique for this type of form. Cylinders are actually clams that exist in many dimensions.

DESIGNING A PARAMETRIC MODEL

We drew the mold in Fusion by setting the basic dimensions: diameter, distance between, cylinders, kerf of the machine.









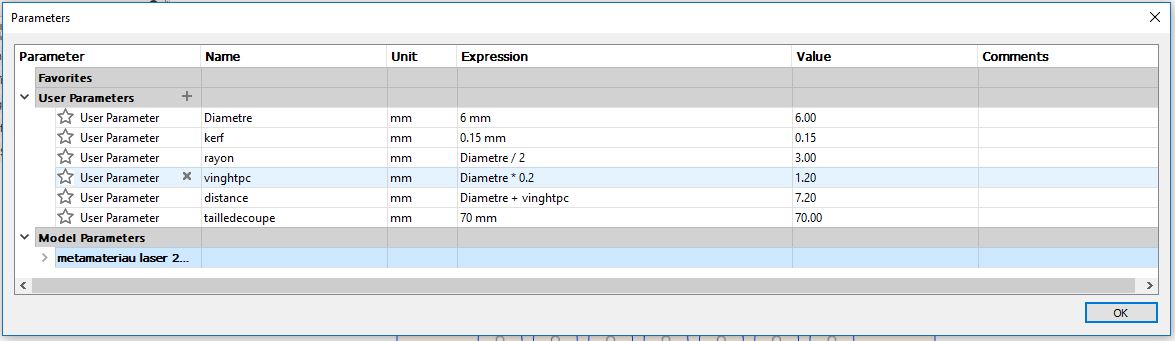
MOULD AND RESIN

We cut out the two forms, the one in which the cylinders will be placed, and the one that holds the resin.



Once that was done, We entered the cylinders into the holes, leveled them, and then sealed the mold with paper.
We used elite double 8 .

There is no particular safety rules for this product.

It is used in a 50/50 mixture, made with a precision balance.



Once the mixture is made, it must be poured in the form of a thin trickle so that there is the least air bubbles.

20 minutes of waiting to open the mould.





Here we are ...



It was a bit fragile on both sides. perhaps it would be necessary to increase the distance between the cylinders,
or the mould was opened too quickly ...

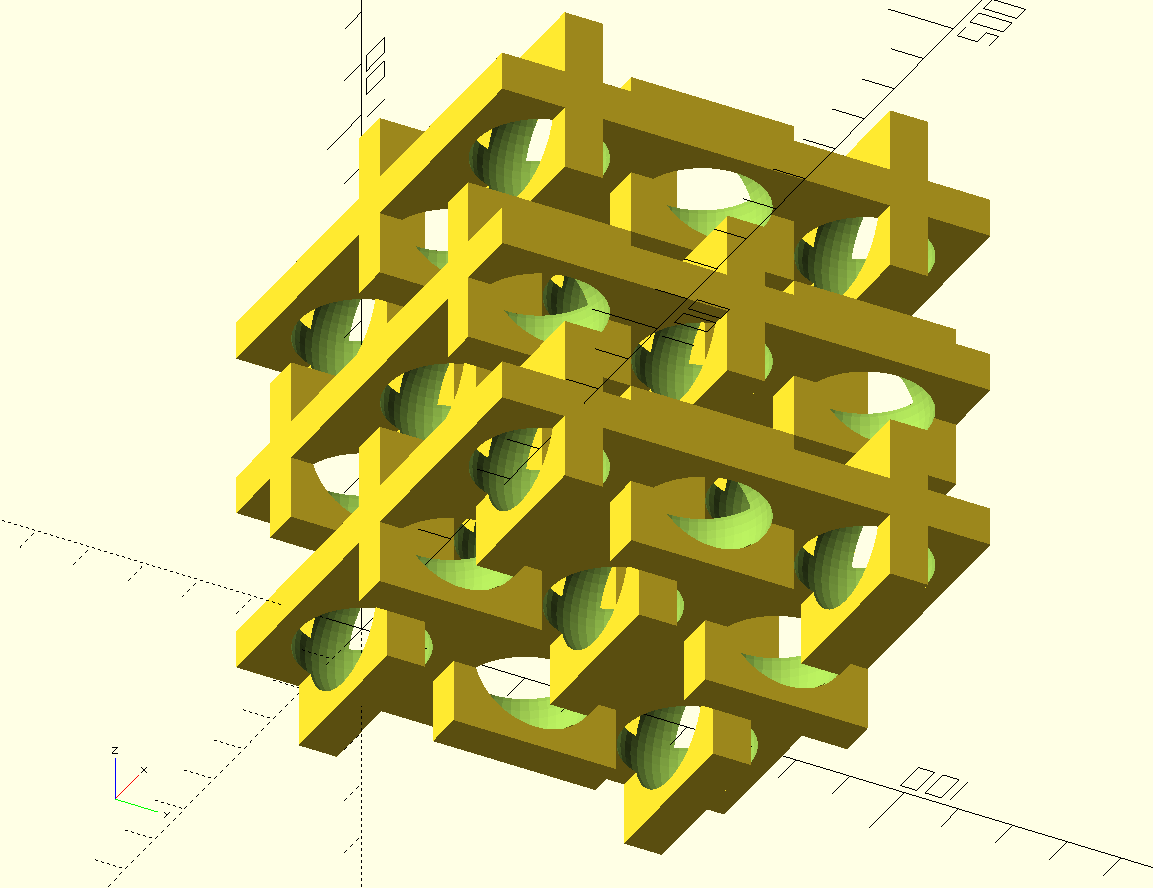
Part III: Molding and casting 3D Mechanical metamaterials

Download file

module_side        = 30;
module_inside_diam = 24;
module_thickness   = 7;
epsilon            = 0.001; //to make sure the negatives are corrects

separate_pieces    = 20;

//$fn=20; //testing purposes
$fn=200; //final rendering

module module_plan_cylinder(){
    difference(){
        cube([module_side+epsilon,module_side+epsilon,module_thickness], center=true);
        cylinder(module_thickness,d=module_inside_diam, center=true);
    }
}

module bi_plan(){
    cube([module_side+epsilon,module_side+epsilon,module_thickness], center=true);
    rotate([90,0,0]) cube([module_side+epsilon,module_side+epsilon,module_thickness], center=true);
}

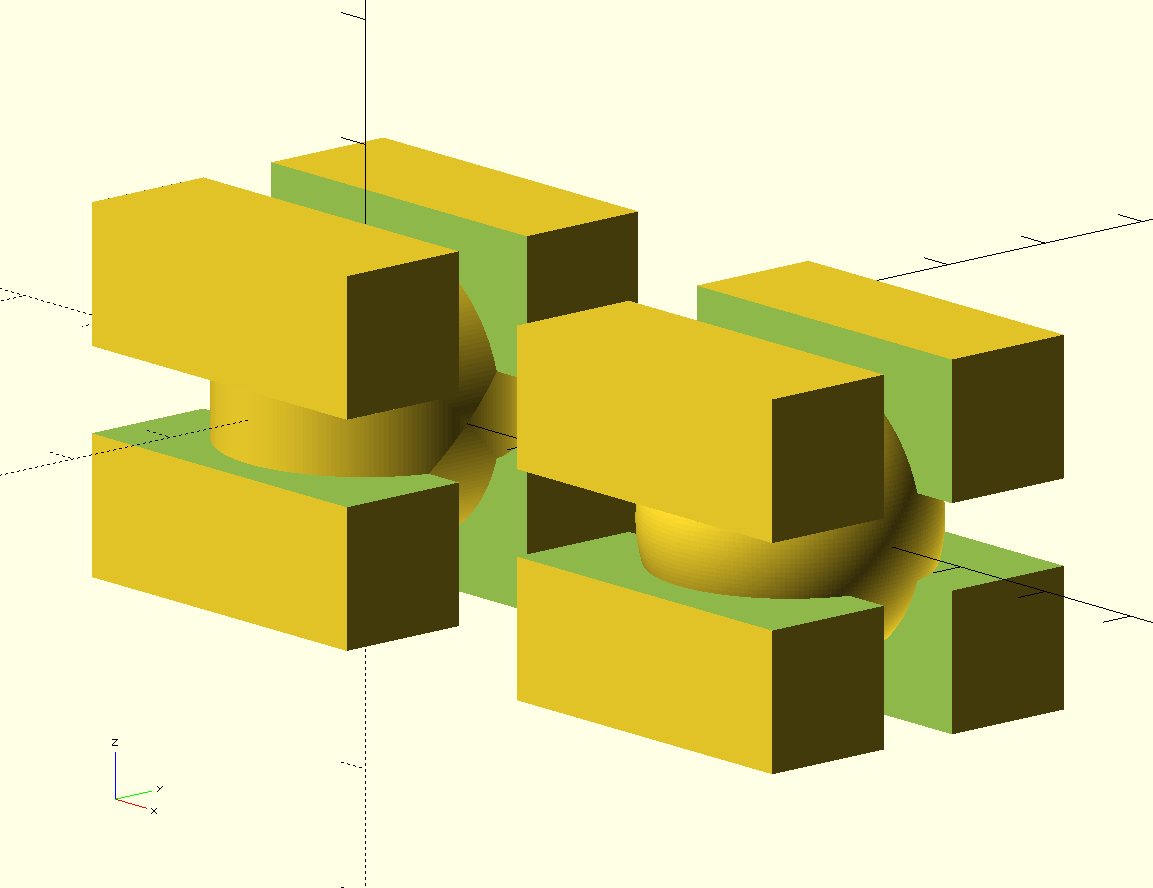
module pixel_cylinder(){
    module_plan_cylinder();
    rotate([90,0,0]) module_plan_cylinder();
}

module pixel_sphere(){
    difference(){
        bi_plan();
        sphere(d=module_inside_diam);
    }
}

module negative(){
    difference(){
        cube(module_side, center=true);
        children();
      }
}

module SeparateChildren(space){
    for ( i= [0:1:$children-1])
      translate([i*space,0,0]) {children(i);}
}

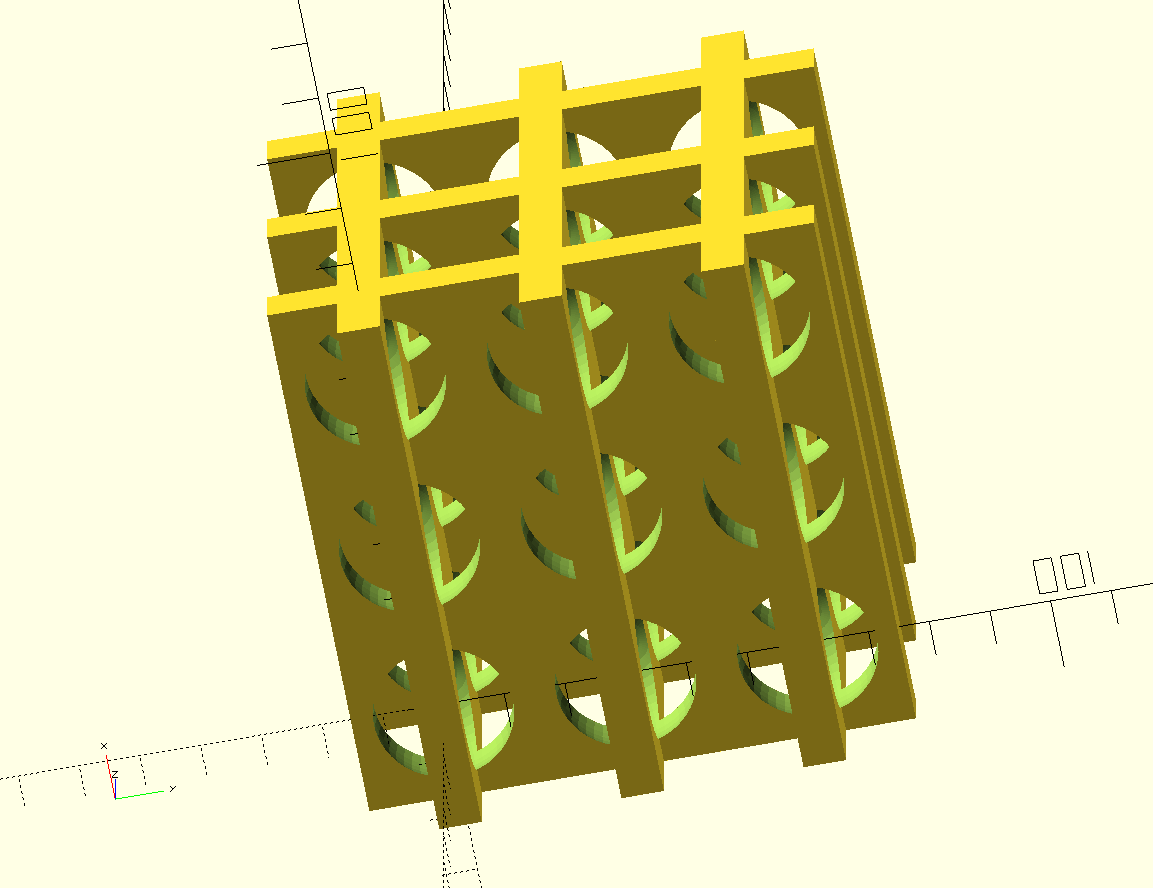
module MatrixModule(x_repeat, y_repeat, z_repeat, alternate){
    for( i = [0:x_repeat-1] ){
        for( j = [0:y_repeat-1] ) {
            for( k = [0:z_repeat-1] ) {
                translate([i*module_side, j*module_side, k*module_side]) rotate([0, 0, (((i+j+k)*alternate)%2)*90]) children();
            }
        }
    }
}

SeparateChildren(module_side+separate_pieces){
    pixel_cylinder();
    pixel_sphere();
    negative(){pixel_cylinder();}
    negative(){pixel_sphere();}
}

//MatrixModule(3,3,3,alternate=1){
//    pixel_sphere();
//}