Fab Lab Barcelona SuperNode /Fab Lab Sevilla /Jose Perez de Lama
Week 03 / 06.02.2013
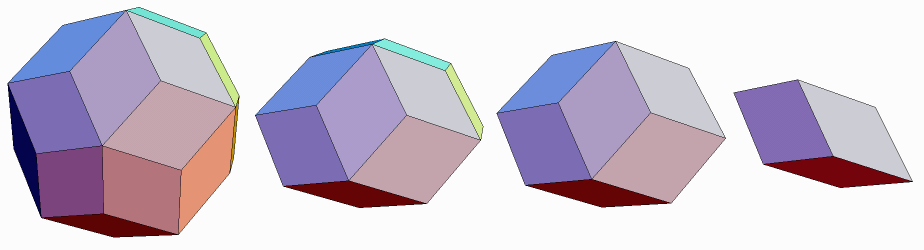
Figure 01: Combinatory with rhombohedra, left to right: triacontrahedrum, 30 faces; golden polipiedro, 20 faces; rhombic dodecahedron, 12 faces; golden rhombohedron prolate, 6 faces. Image source unknown: published in the Internet
[assignment]
Design and fabricate a press-fit construction kit to vinyl-or-laser cut; using a parametric design tool [Inkscape, Rhino & Grasshopper, OpenSCAD, Kokopelli or fabserver]. The kit pieces should allow for the construction of multiple combinations.
Link to class syllabus:
http://academy.cba.mit.edu/classes/computer_cutting/index.html
[assignment development]
Typically a construction kit to allow for different configurations is based on a spatial grid, that contributes with a certain "metrology" and combination/growth rules.
I decided to base my design on previous geometric studies developed under professor Antonio Saseta, a good friend at the School of Architecture in Sevilla. He is very fascinated with "aperiodic" plane and space tiling systems, in particular with those based on Roger Penrose's and Robert Ammann's work, that deal with particular rhombs and rhombohedra connected to the regular pentagon, dodecahedron and icosahedron, and the Fi constant,- which we can find in the regular pentagon's diagonal. These tilings are said to be aperiodic because they don't repeat themselves by translation as periodic tilings do, but by translation + rotation (in angles which are those found in the dodecahedron and icosahedron]. Architect Daniel Libeskind together with Cecil Balmond applied a beautiful aperiodic tiling system in the fassade of their project for the Victoria and Albert Museum in London, - still to be built [Cecile Balmond, 2008, Informal].
[Penrose rhombs and golden rhombohedra]
The so called "golden rhombohedra" [two of them] where invented, or discovered, by Robert Ammann [1946-1994] in 1975 [http://en.wikipedia.org/wiki/Robert_Ammann]. Ammann, at the time almost a homeless, was an amateur mathematician, who reminds us of Kilgore Trout, the Kurt Vonnegut character. Apologies if this might seem to be a very free mental association: http://en.wikipedia.org/wiki/Kilgore_Trout].
Penrose rhombs are two complementary ones, by themselves, and together in several variations, they can tile the plane. Their edge angles are fascinating: 36, 72, 108, 144 (that is 2*Pi/10, 4*Pi/10, 6*Pi/10 and 8*Pi/10). These angles become the dihedral angles of Ammann's or "golden" rhombohedra. One can find Penrose rhombs in the diagonals of the two Ammann rhombohedra, but their faces, all of them equal are not Penrose rhombs, but golden rhombs, that is rhombs whose diagonals are in a Fi proportion [http://en.wikipedia.org/wiki/Golden_rhombus]. See Figure 2:
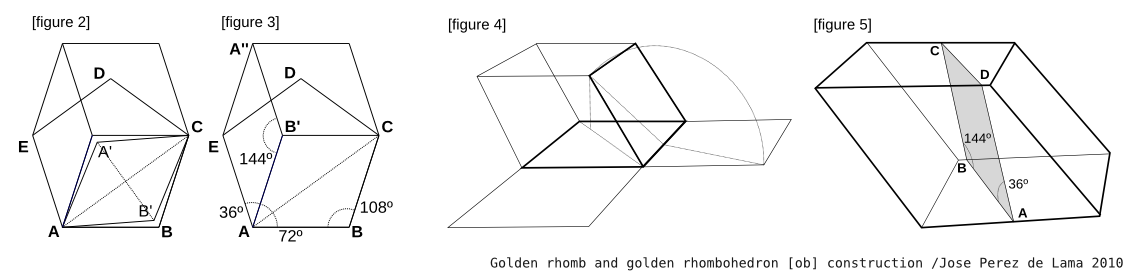
Golden rhombohedra can tile or pack space, that is fill it without leaving empty spaces, as said, with 3D symmetries that are those found in the icosahedron. These geometries are tricky to visualize, but are interesting therefore because they look to an observer like chaotic but do have a strict geometric order.
As can be read in Wikipedia, the discovery in 1982 of "quasicrystals", whose atomic geometry is arranged acording to aperiodic patterns, gave Ammann's discovery a great relevance.
[sketching a press-fit construction system based on golden rhombohedra]
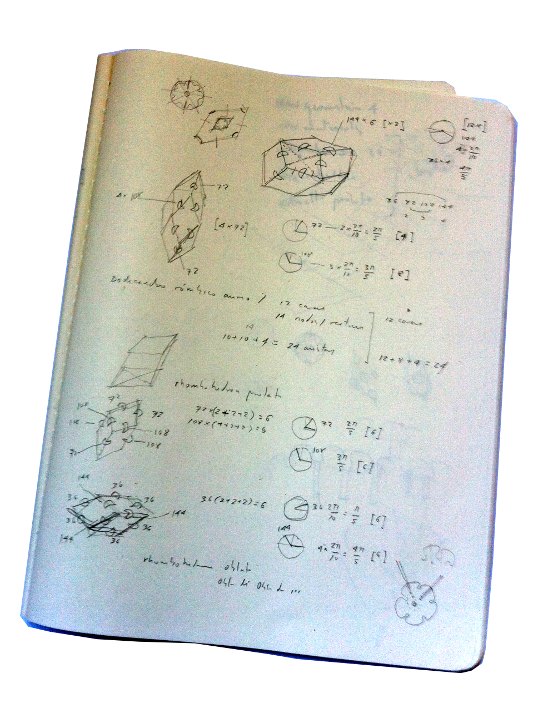
Figure 03: Notebook; counting nodes, edges and faces; and angles.
Even if it is difficult to visualize and therefore 3D model aperiodic geometric grids, when it comes to a construction kit it becomes paradoxically simple.
The system designed now is based on building polyhedra using faces and edges [there are at least three possibilites two build 3D grids with planar pieces: building them with nodes and edges, which is the most obvious, with nodes and faces, and the one used here].
The actual construction kit is composed by pieces corresponding to the faces [golden rhombs] which are all of them the same, with the same cut-outs; and pieces corresponding to the edges. The pieces corresponding to the edges are designed now as circles with cut-outs. As showed by professor Saseta we could use a single piece for the edges to build the whole system. This piece would have 10 regularly distributed cut-outs [each with a 36º, 2*Pi/10, angle of each other]. However, for this design i have used 4 different pieces, each with two cut-outs, placed respectively at 36º, 72º, 108º and 144º. After several tests i think this makes construction easier.
6*rhombs + 6*(36º-circle-pieces) + 6*(144º-circle-pieces) make an oblate golden rhombohedron
6*rhombs + 6*(72º-circle-pieces) + 6*(108º-circle-pieces) make a prolate golden rhombohedron
12*rhombs + 12*(144º-circle-pieces) + 8*(108º-circle-pieces) + [4*(72º-circle-pieces) make a rhombic dodecahedron
And so on [as K. Vonnegut would say].
To understand how the combination works it was very useful to have paper laser-cut models of the polihedra that we had around in the lab:
Figure 04: 3D printed ring with rhombohedron, designed by JPL 2010. Downloadable in Thingiverse: http://www.thingiverse.com/thing:5398
[process & troubleshooting]
Having some previous experience with 3D modelling golden rhombohedra, making fold-up models and building various regular-periodic grids with the laser cutter, i thought the process was going to be fast and lean. I decided to beging with 3D modelling the rhombohedra with Rhinoceros, very roughly, - an afterwards try to model the planar pieces with fabserver. Based on the Rhino generated dxf files i cut a fast test in thin DMF, which was available in the lab... But the pieces didn't fit as i had supposed... [figure...] I had assumed the cut-outs were going to be in the center of the faces, but once you offset the faces a bit to be able to fit the joints (circles), because of the skewed geometry, the cut-outs don't fall in the middle of the edges anymore... This took me a while to understand...


Figures 05 & 06: Playing with paper rhombohedra; built by Antonio Saseta, Ángel Linares and José Buzón, Fab Lab Sevilla 2010. The blue ones are oblate or low rhombohedra, while the yellow ones are tall, acute or prolate rhomboedra. The two of them, low and tall, are made with the same pieces, 6 golden rhombs, put together in different angles. Right image: two low + two tall rhombohedra pur together to make a golden rhombic dedecahedron.
So, i redrew them with more detail, and then i moved on to define them with Grasshopper. Even if the piece is simple, because the angles are not "periodic", that is not the same, the list management became a bit tricky. I ended up with not a very intelligent [graphic] definition, but one that worked. When dealing with polyhedra it is very good, if not necessary, to have lists with the nodes, edges and faces of the polyhedra. It would be even better to have another list with the rotation+translation operatores in order to generate the grids; but this i haven't managed yet...
The intersection algorithm in my Rhino 4.0 SR9 / Grasshopper 0.9.0014 is a little buggy. When you move the sliders some intersections change from line to polyline, and therefore the list of points it generates changes, and makes the definition not to work properly. I tried several alternatives to manage the intersection, and now it is reasonably efficient. This made me think of course, of the difference between cad software using b-rep and f-rep, explained by NG in the second class.
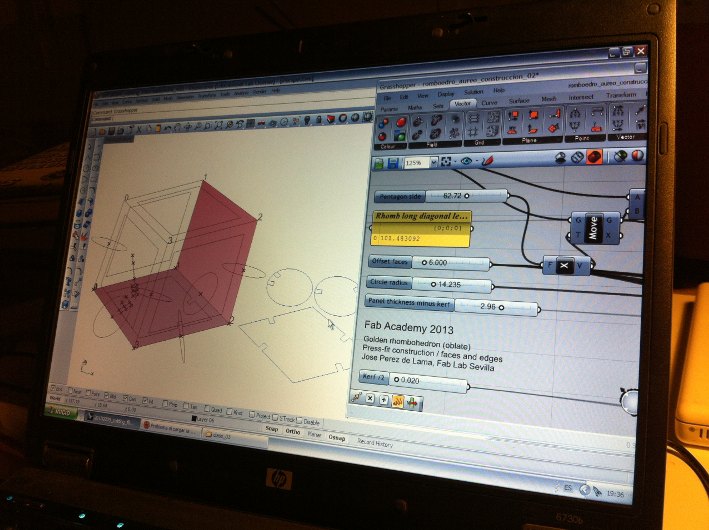
Figure 07: Screenshot with Grasshopper definition. The cutting files of the three pieces can be seen to the right of the 3D diagrammatic model. On the right part of the screen: the sliders with parameters used to generate different instances; parameters include dimensions of the model, panel thickness and kerf.
The definition right now generates the geometry and cutting files for one of the two rhombohedra (the so called oblate one). I have also a definition for the tall or prolate one, but i haven't generated parametric cutting files yet. The definition as it is right now accepts the following parameters:
# Pentagon side (mm) :: side of the pentagon that is used as the base for the whole construction. This gives me in the same panel the long diagonal of the face which is the main dimension of the units.
# Faces offset
# Circle radius
# Panel thickness (minus kerf)
# Kerf :: right now the co-relation between these two latter parameters i have to introduce by hand; i still need to interconnect them in the definition.
It outputs cutting files for the three pieces used to build the "oblate rhombohedron".
With minor changes in Rhinoceros [angles of cut-outs in the circle-pieces] i have drawn the files to build the "prolate rhombohedron", and further combinations.
-
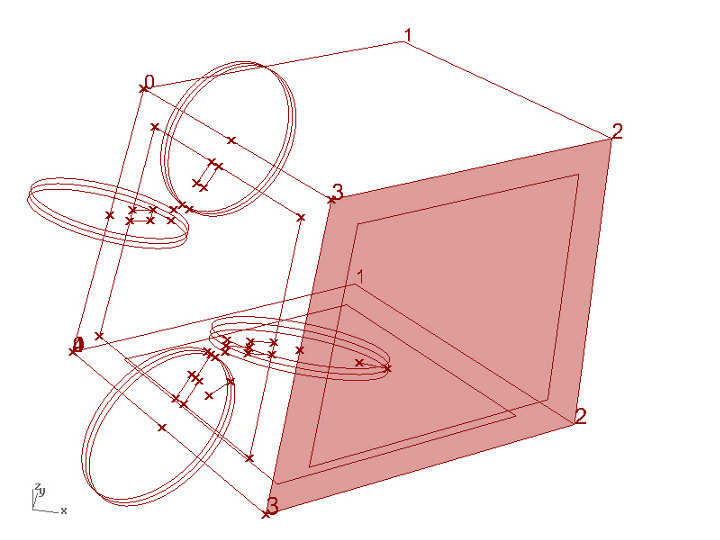
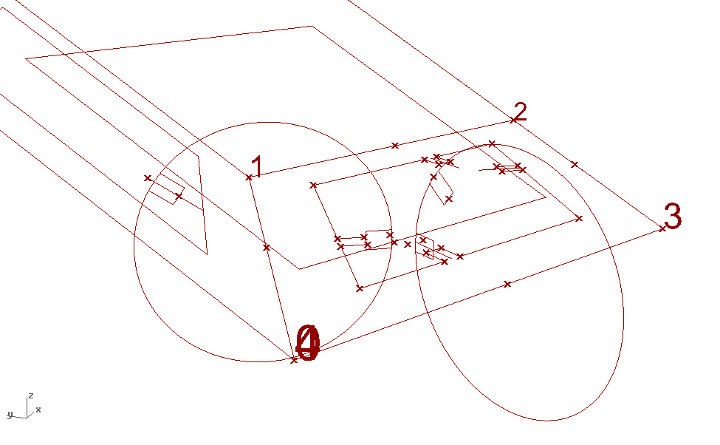
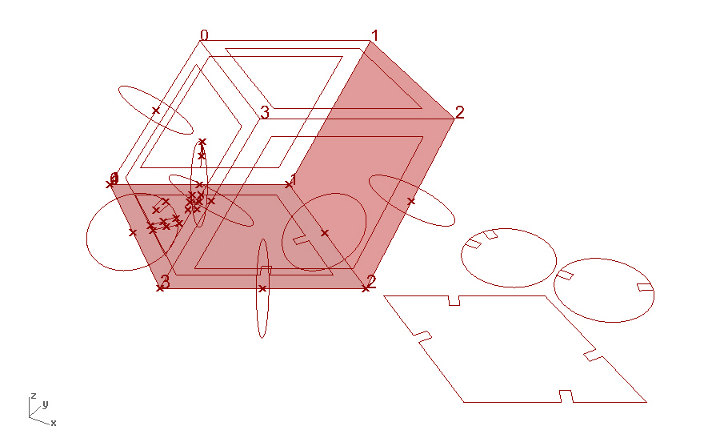
Figures 08, 09, 10: Grasshopper screenshots; 08: geometry, faces offset and circle join pieces; 09: parametric definition of join cut-outs; 10: projection in C-plane of planar pieces; cutting files.


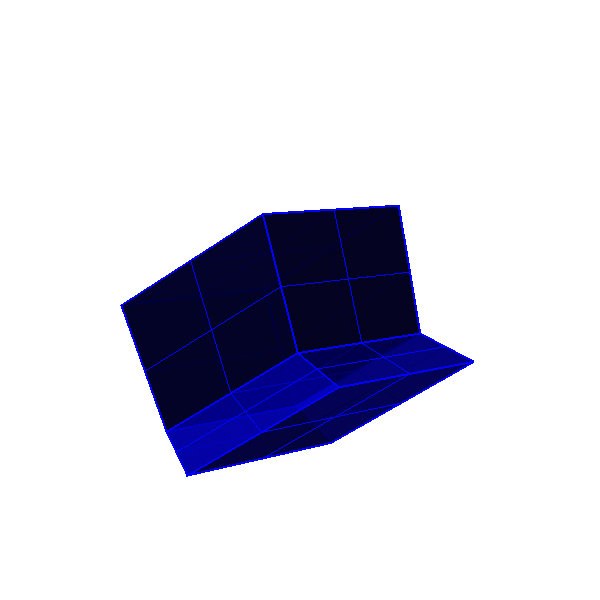
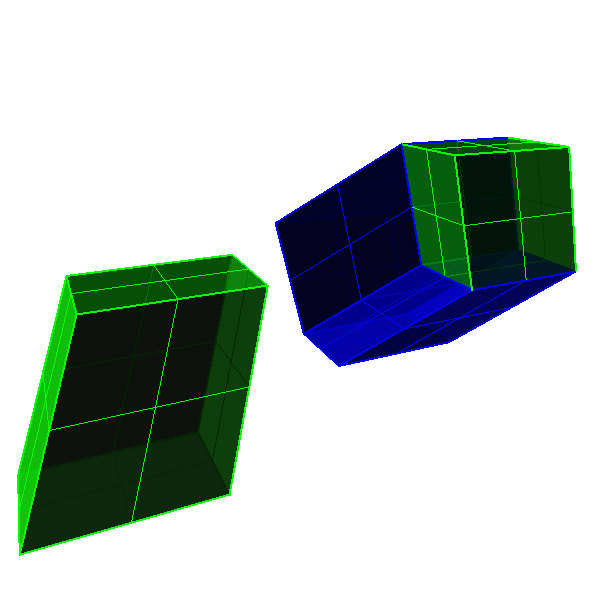
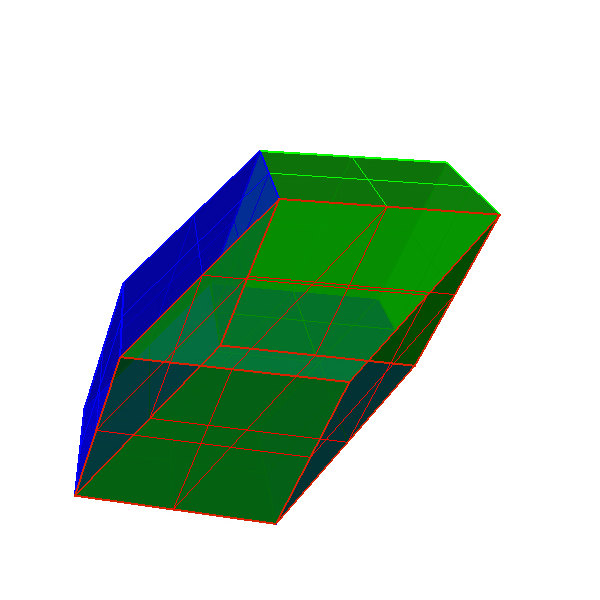

Figure 11:Rhombohedra composition; two oblate golden rhombohedra [blue] + two prolate rhombohedra [green] make a rhombic golden dodecahedron. Basic geometry with grasshopper; composition with Rhinoceros.
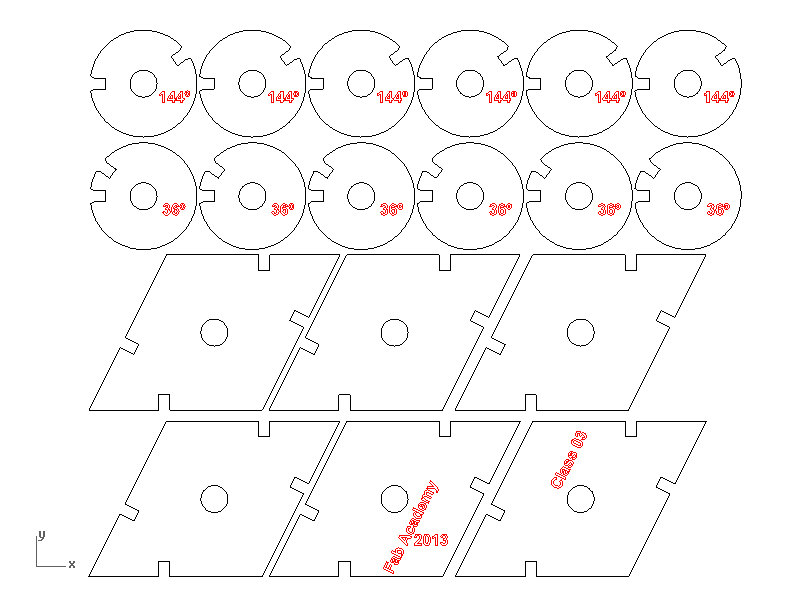
Figure 12: Golden rhombohedron, oblate, cutting files; Grasshopper and Rhinoceros
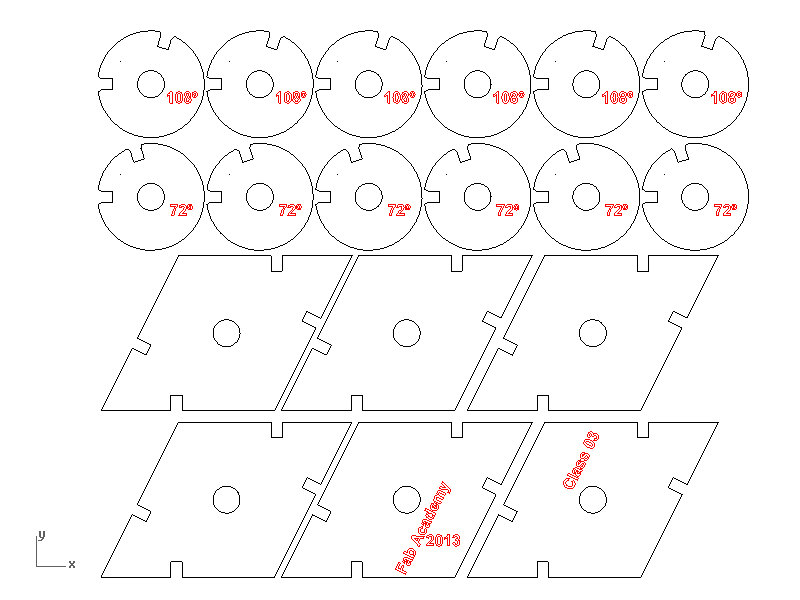
Figure 13: Golden rhombohedron prolate, cutting files; Grasshopper and Rhinoceros
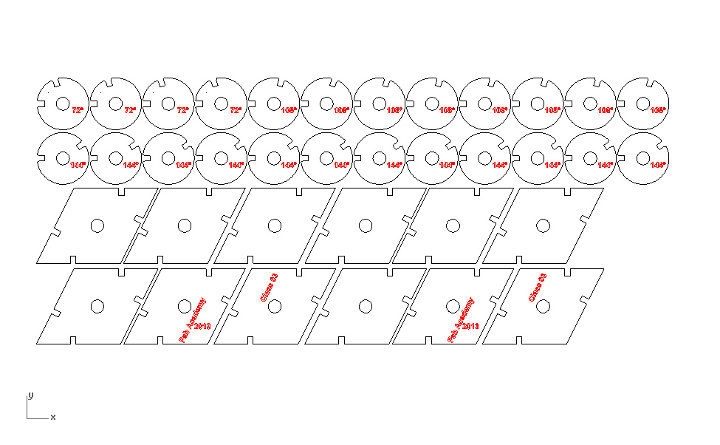
Figure 14: Rhombic golden dodecahedron cutting files; Grasshopper and Rhinoceros
///
[laser cutting and assembling]


Figures 15 & 16: Tests with press-fit low and tall rhombohedra. The cut-out design of the joins was not well placed in these tests. JPL with Jose Buzón and Juan Carlos Pérez.
Then i cut a final version, with pieces to put together the two golden rhombohedra, and a rhimbic dodecahedron, the three of them using the same set of pieces. Besides these well known polyhedra the system can be used to build various shapes...
Here are images of the process and the final pieces:


Figures 17 & 18: Set of planar pieces. On the right the four different "edge" pieces are shown with 36, 72, 108 and 144 angled cut-outs. The "face" pieces are all the same for every combination.


Figures 19 & 20: Prolate [tall] golden rhombohedron, made out of 6 rhombic "faces", 6 * 72ª join circles and 6 * 108º join circles, both of them corresponding to the edges of the polyhedrum.


Figures 21 & 22: Oblate [low] golden rhombohedron; left under construction, right complete. It si made again of the same 6 rhombic faces, but then with 6 * 36º join circles and 6 * 144º join circles.


Figures 23 & 24: Golden rhombic dodecahedron. This piece is made putting together two oblate and two prolate rhombohedra. This one is built only with the outside faces; using 12 * rhombic faces, 12 * 144º circle joins, 8 * 108º circle joins and 4 * 72º circle joins.
[kokopelli and fabserver]
I still will try to 2D model the pieces with kokopelli and/or fabserver. I think i know how to make the circle piece, making changes to the compass.cad file. I need to do a little experimentation to generate the exact angles of the rhombic faces and cut-outs. There is a rhomb generation procedure in the same file that i believe i could use, too. These angles, are not part of the 36-72-108 series, so using a numeric system to introduce coordinates rather than actually obtaining the golden rhomb through geometric procedures based on the regular pentagon might impair precission...
[files download]
Design files are downnloadable under a Creative Commons Attribution-Share A Like license

# Golden rhombohedron oblate, faces and edges construction; [.gh / still buggy]
# Golden rhombohedron oblate, prolate & dodecahedron laser cutting files; [.3dm; .dxf]
Cutting files are designed for 2.98 mm thickness dmf panels, and a kerf of 0.2 mm
return home /perezdelama.jose